Exercise Categories
Lists
Tail of a List Last Two Elements of a List N'th Element of a List Length of a List Reverse a List Palindrome Flatten a List Eliminate Duplicates Pack Consecutive Duplicates Run-Length Encoding Modified Run-Length Encoding Decode a Run-Length Encoded List Run-Length Encoding of a List (Direct Solution) Duplicate the Elements of a List Replicate the Elements of a List a Given Number of Times Drop Every N'th Element From a List Split a List Into Two Parts; The Length of the First Part Is Given Extract a Slice From a List Rotate a List N Places to the Left Remove the K'th Element From a List Insert an Element at a Given Position Into a List Create a List Containing All Integers Within a Given Range Extract a Given Number of Randomly Selected Elements From a List Lotto: Draw N Different Random Numbers From the Set 1..M Generate a Random Permutation of the Elements of a List Generate the Combinations of K Distinct Objects Chosen From the N Elements of a List Group the Elements of a Set Into Disjoint Subsets Sorting a List of Lists According to Length of SublistsArithmetic
Determine Whether a Given Integer Number Is Prime Determine the Greatest Common Divisor of Two Positive Integer Numbers Determine Whether Two Positive Integer Numbers Are Coprime Calculate Euler's Totient Function Φ(m) Determine the Prime Factors of a Given Positive Integer Determine the Prime Factors of a Given Positive Integer (2) Calculate Euler's Totient Function Φ(m) (Improved) Compare the Two Methods of Calculating Euler's Totient Function A List of Prime Numbers Goldbach's Conjecture A List of Goldbach CompositionsLogic and Codes
Truth Tables for Logical Expressions (2 Variables) Truth Tables for Logical Expressions Gray Code Huffman CodeBinary Trees
Construct Completely Balanced Binary Trees Symmetric Binary Trees Binary Search Trees (Dictionaries) Generate-and-Test Paradigm Construct Height-Balanced Binary Trees Construct Height-Balanced Binary Trees With a Given Number of Nodes Count the Leaves of a Binary Tree Collect the Leaves of a Binary Tree in a List Collect the Internal Nodes of a Binary Tree in a List Collect the Nodes at a Given Level in a List Construct a Complete Binary Tree Layout a Binary Tree (1) Layout a Binary Tree (2) Layout a Binary Tree (3) A String Representation of Binary Trees Preorder and Inorder Sequences of Binary Trees Dotstring Representation of Binary TreesMultiway Trees
Tree Construction From a Node String Count the Nodes of a Multiway Tree Determine the Internal Path Length of a Tree Construct the Bottom-Up Order Sequence of the Tree Nodes Lisp-Like Tree RepresentationGraphs
Conversions Path From One Node to Another One Cycle From a Given Node Construct All Spanning Trees Construct the Minimal Spanning Tree Graph Isomorphism Node Degree and Graph Coloration Depth-First Order Graph Traversal Connected Components Bipartite Graphs Generate K-Regular Simple Graphs With N NodesExercises
This section is inspired by Ninety-Nine Lisp Problems which in turn was based on “Prolog problem list” by Werner Hett. For each of these questions, some simple tests are shown—they may also serve to make the question clearer if needed. To work on these problems, we recommend you first install OCaml or use it inside your browser. The source of the following problems is available on GitHub.
Every exercise has a difficulty level, ranging from beginner to advanced.
Tail of a List
Write a function last : 'a list -> 'a option that returns the last element of a list
# last ["a" ; "b" ; "c" ; "d"];;
- : string option = Some "d"
# last [];;
- : 'a option = None
# let rec last = function
| [] -> None
| [ x ] -> Some x
| _ :: t -> last t;;
val last : 'a list -> 'a option = <fun>
Last Two Elements of a List
Find the last two (last and penultimate) elements of a list.
# last_two ["a"; "b"; "c"; "d"];;
- : (string * string) option = Some ("c", "d")
# last_two ["a"];;
- : (string * string) option = None
# let rec last_two = function
| [] | [_] -> None
| [x; y] -> Some (x,y)
| _ :: t -> last_two t;;
val last_two : 'a list -> ('a * 'a) option = <fun>
N'th Element of a List
Find the N'th element of a list.
# at 2 ["a"; "b"; "c"; "d"; "e"];;
- : string option = Some "c"
# at 2 ["a"];;
- : string option = None
Remark: OCaml has List.nth which numbers elements from 0 and
raises an exception if the index is out of bounds.
# List.nth ["a"; "b"; "c"; "d"; "e"] 2;;
- : string = "c"
# List.nth ["a"] 2;;
Exception: Failure "nth".
# let rec at k = function
| [] -> None
| h :: t -> if k = 0 then Some h else at (k - 1) t;;
val at : int -> 'a list -> 'a option = <fun>
Length of a List
Find the number of elements of a list.
OCaml standard library has List.length but we ask that you reimplement
it. Bonus for a tail recursive
solution.
# length ["a"; "b"; "c"];;
- : int = 3
# length [];;
- : int = 0
This function is tail-recursive: it uses a constant amount of stack memory regardless of list size.
# let length list =
let rec aux n = function
| [] -> n
| _ :: t -> aux (n + 1) t
in
aux 0 list;;
val length : 'a list -> int = <fun>
Reverse a List
Reverse a list.
OCaml standard library has List.rev but we ask that you reimplement
it.
# rev ["a"; "b"; "c"];;
- : string list = ["c"; "b"; "a"]
# let rev list =
let rec aux acc = function
| [] -> acc
| h :: t -> aux (h :: acc) t
in
aux [] list;;
val rev : 'a list -> 'a list = <fun>
Palindrome
Find out whether a list is a palindrome.
Hint: A palindrome is its own reverse.
# is_palindrome ["x"; "a"; "m"; "a"; "x"];;
- : bool = true
# not (is_palindrome ["a"; "b"]);;
- : bool = true
# let is_palindrome list =
(* One can use either the rev function from the previous problem, or the built-in List.rev *)
list = List.rev list;;
val is_palindrome : 'a list -> bool = <fun>
Flatten a List
Flatten a nested list structure.
type 'a node =
| One of 'a
| Many of 'a node list
# flatten [One "a"; Many [One "b"; Many [One "c" ;One "d"]; One "e"]];;
- : string list = ["a"; "b"; "c"; "d"; "e"]
# type 'a node =
| One of 'a
| Many of 'a node list;;
type 'a node = One of 'a | Many of 'a node list
# (* This function traverses the list, prepending any encountered elements
to an accumulator, which flattens the list in inverse order. It can
then be reversed to obtain the actual flattened list. *);;
# let flatten list =
let rec aux acc = function
| [] -> acc
| One x :: t -> aux (x :: acc) t
| Many l :: t -> aux (aux acc l) t
in
List.rev (aux [] list);;
val flatten : 'a node list -> 'a list = <fun>
Eliminate Duplicates
Eliminate consecutive duplicates of list elements.
# compress ["a"; "a"; "a"; "a"; "b"; "c"; "c"; "a"; "a"; "d"; "e"; "e"; "e"; "e"];;
- : string list = ["a"; "b"; "c"; "a"; "d"; "e"]
# let rec compress = function
| a :: (b :: _ as t) -> if a = b then compress t else a :: compress t
| smaller -> smaller;;
val compress : 'a list -> 'a list = <fun>
Pack Consecutive Duplicates
Pack consecutive duplicates of list elements into sublists.
# pack ["a"; "a"; "a"; "a"; "b"; "c"; "c"; "a"; "a"; "d"; "d"; "e"; "e"; "e"; "e"];;
- : string list list =
[["a"; "a"; "a"; "a"]; ["b"]; ["c"; "c"]; ["a"; "a"]; ["d"; "d"];
["e"; "e"; "e"; "e"]]
# let pack list =
let rec aux current acc = function
| [] -> [] (* Can only be reached if original list is empty *)
| [x] -> (x :: current) :: acc
| a :: (b :: _ as t) ->
if a = b then aux (a :: current) acc t
else aux [] ((a :: current) :: acc) t in
List.rev (aux [] [] list);;
val pack : 'a list -> 'a list list = <fun>
Run-Length Encoding
If you need so, refresh your memory about run-length encoding.
Here is an example:
# encode ["a"; "a"; "a"; "a"; "b"; "c"; "c"; "a"; "a"; "d"; "e"; "e"; "e"; "e"];;
- : (int * string) list =
[(4, "a"); (1, "b"); (2, "c"); (2, "a"); (1, "d"); (4, "e")]
# let encode list =
let rec aux count acc = function
| [] -> [] (* Can only be reached if original list is empty *)
| [x] -> (count + 1, x) :: acc
| a :: (b :: _ as t) -> if a = b then aux (count + 1) acc t
else aux 0 ((count + 1, a) :: acc) t in
List.rev (aux 0 [] list);;
val encode : 'a list -> (int * 'a) list = <fun>
An alternative solution, which is shorter but requires more memory, is to use
the pack function declared in problem 9:
# let pack list =
let rec aux current acc = function
| [] -> [] (* Can only be reached if original list is empty *)
| [x] -> (x :: current) :: acc
| a :: (b :: _ as t) ->
if a = b then aux (a :: current) acc t
else aux [] ((a :: current) :: acc) t in
List.rev (aux [] [] list);;
val pack : 'a list -> 'a list list = <fun>
# let encode list =
List.map (fun l -> (List.length l, List.hd l)) (pack list);;
val encode : 'a list -> (int * 'a) list = <fun>
Modified Run-Length Encoding
Modify the result of the previous problem in such a way that if an element has no duplicates it is simply copied into the result list. Only elements with duplicates are transferred as (N E) lists.
Since OCaml lists are homogeneous, one needs to define a type to hold both single elements and sub-lists.
type 'a rle =
| One of 'a
| Many of int * 'a
# encode ["a"; "a"; "a"; "a"; "b"; "c"; "c"; "a"; "a"; "d"; "e"; "e"; "e"; "e"];;
- : string rle list =
[Many (4, "a"); One "b"; Many (2, "c"); Many (2, "a"); One "d";
Many (4, "e")]
# type 'a rle =
| One of 'a
| Many of int * 'a;;
type 'a rle = One of 'a | Many of int * 'a
# let encode l =
let create_tuple cnt elem =
if cnt = 1 then One elem
else Many (cnt, elem) in
let rec aux count acc = function
| [] -> []
| [x] -> (create_tuple (count + 1) x) :: acc
| hd :: (snd :: _ as tl) ->
if hd = snd then aux (count + 1) acc tl
else aux 0 ((create_tuple (count + 1) hd) :: acc) tl in
List.rev (aux 0 [] l);;
val encode : 'a list -> 'a rle list = <fun>
Decode a Run-Length Encoded List
Given a run-length code list generated as specified in the previous problem, construct its uncompressed version.
# decode [Many (4, "a"); One "b"; Many (2, "c"); Many (2, "a"); One "d"; Many (4, "e")];;
- : string list =
["a"; "a"; "a"; "a"; "b"; "c"; "c"; "a"; "a"; "d"; "e"; "e"; "e"; "e"]
# let decode list =
let rec many acc n x =
if n = 0 then acc else many (x :: acc) (n - 1) x
in
let rec aux acc = function
| [] -> acc
| One x :: t -> aux (x :: acc) t
| Many (n, x) :: t -> aux (many acc n x) t
in
aux [] (List.rev list);;
val decode : 'a rle list -> 'a list = <fun>
Run-Length Encoding of a List (Direct Solution)
Implement the so-called run-length encoding data compression method directly. I.e. don't explicitly create the sublists containing the duplicates, as in problem "Pack consecutive duplicates of list elements into sublists", but only count them. As in problem "Modified run-length encoding", simplify the result list by replacing the singleton lists (1 X) by X.
# encode ["a";"a";"a";"a";"b";"c";"c";"a";"a";"d";"e";"e";"e";"e"];;
- : string rle list =
[Many (4, "a"); One "b"; Many (2, "c"); Many (2, "a"); One "d";
Many (4, "e")]
# let encode list =
let rle count x = if count = 0 then One x else Many (count + 1, x) in
let rec aux count acc = function
| [] -> [] (* Can only be reached if original list is empty *)
| [x] -> rle count x :: acc
| a :: (b :: _ as t) -> if a = b then aux (count + 1) acc t
else aux 0 (rle count a :: acc) t
in
List.rev (aux 0 [] list);;
val encode : 'a list -> 'a rle list = <fun>
Duplicate the Elements of a List
Duplicate the elements of a list.
# duplicate ["a"; "b"; "c"; "c"; "d"];;
- : string list = ["a"; "a"; "b"; "b"; "c"; "c"; "c"; "c"; "d"; "d"]
# let rec duplicate = function
| [] -> []
| h :: t -> h :: h :: duplicate t;;
val duplicate : 'a list -> 'a list = <fun>
Remark: this function is not tail recursive. Can you modify it so it becomes so?
Replicate the Elements of a List a Given Number of Times
Replicate the elements of a list a given number of times.
# replicate ["a"; "b"; "c"] 3;;
- : string list = ["a"; "a"; "a"; "b"; "b"; "b"; "c"; "c"; "c"]
# let replicate list n =
let rec prepend n acc x =
if n = 0 then acc else prepend (n-1) (x :: acc) x in
let rec aux acc = function
| [] -> acc
| h :: t -> aux (prepend n acc h) t in
(* This could also be written as:
List.fold_left (prepend n) [] (List.rev list) *)
aux [] (List.rev list);;
val replicate : 'a list -> int -> 'a list = <fun>
Note that
List.rev listis needed only because we wantauxto be tail recursive.
Drop Every N'th Element From a List
Drop every N'th element from a list.
# drop ["a"; "b"; "c"; "d"; "e"; "f"; "g"; "h"; "i"; "j"] 3;;
- : string list = ["a"; "b"; "d"; "e"; "g"; "h"; "j"]
# let drop list n =
let rec aux i = function
| [] -> []
| h :: t -> if i = n then aux 1 t else h :: aux (i + 1) t in
aux 1 list;;
val drop : 'a list -> int -> 'a list = <fun>
Split a List Into Two Parts; The Length of the First Part Is Given
Split a list into two parts; the length of the first part is given.
If the length of the first part is longer than the entire list, then the first part is the list and the second part is empty.
# split ["a"; "b"; "c"; "d"; "e"; "f"; "g"; "h"; "i"; "j"] 3;;
- : string list * string list =
(["a"; "b"; "c"], ["d"; "e"; "f"; "g"; "h"; "i"; "j"])
# split ["a"; "b"; "c"; "d"] 5;;
- : string list * string list = (["a"; "b"; "c"; "d"], [])
# let split list n =
let rec aux i acc = function
| [] -> List.rev acc, []
| h :: t as l -> if i = 0 then List.rev acc, l
else aux (i - 1) (h :: acc) t
in
aux n [] list;;
val split : 'a list -> int -> 'a list * 'a list = <fun>
Extract a Slice From a List
Given two indices, i and k, the slice is the list containing the
elements between the i'th and k'th element of the original list
(both limits included). Start counting the elements with 0 (this is the
way the List module numbers elements).
# slice ["a"; "b"; "c"; "d"; "e"; "f"; "g"; "h"; "i"; "j"] 2 6;;
- : string list = ["c"; "d"; "e"; "f"; "g"]
# let slice list i k =
let rec take n = function
| [] -> []
| h :: t -> if n = 0 then [] else h :: take (n - 1) t
in
let rec drop n = function
| [] -> []
| h :: t as l -> if n = 0 then l else drop (n - 1) t
in
take (k - i + 1) (drop i list);;
val slice : 'a list -> int -> int -> 'a list = <fun>
This solution has a drawback, namely that the take function is not
tail recursive so it may
exhaust the stack when given a very long list. You may also notice that
the structure of take and drop is similar and you may want to
abstract their common skeleton in a single function. Here is a solution.
# let rec fold_until f acc n = function
| [] -> (acc, [])
| h :: t as l -> if n = 0 then (acc, l)
else fold_until f (f acc h) (n - 1) t
let slice list i k =
let _, list = fold_until (fun _ _ -> []) [] i list in
let taken, _ = fold_until (fun acc h -> h :: acc) [] (k - i + 1) list in
List.rev taken;;
val fold_until : ('a -> 'b -> 'a) -> 'a -> int -> 'b list -> 'a * 'b list =
<fun>
val slice : 'a list -> int -> int -> 'a list = <fun>
Rotate a List N Places to the Left
Rotate a list N places to the left.
# rotate ["a"; "b"; "c"; "d"; "e"; "f"; "g"; "h"] 3;;
- : string list = ["d"; "e"; "f"; "g"; "h"; "a"; "b"; "c"]
# let split list n =
let rec aux i acc = function
| [] -> List.rev acc, []
| h :: t as l -> if i = 0 then List.rev acc, l
else aux (i - 1) (h :: acc) t in
aux n [] list
let rotate list n =
let len = List.length list in
(* Compute a rotation value between 0 and len - 1 *)
let n = if len = 0 then 0 else (n mod len + len) mod len in
if n = 0 then list
else let a, b = split list n in b @ a;;
val split : 'a list -> int -> 'a list * 'a list = <fun>
val rotate : 'a list -> int -> 'a list = <fun>
Remove the K'th Element From a List
Remove the K'th element from a list.
The first element of the list is numbered 0, the second 1,...
# remove_at 1 ["a"; "b"; "c"; "d"];;
- : string list = ["a"; "c"; "d"]
# let rec remove_at n = function
| [] -> []
| h :: t -> if n = 0 then t else h :: remove_at (n - 1) t;;
val remove_at : int -> 'a list -> 'a list = <fun>
Insert an Element at a Given Position Into a List
Start counting list elements with 0. If the position is larger or equal to the length of the list, insert the element at the end. (The behavior is unspecified if the position is negative.)
# insert_at "alfa" 1 ["a"; "b"; "c"; "d"];;
- : string list = ["a"; "alfa"; "b"; "c"; "d"]
# let rec insert_at x n = function
| [] -> [x]
| h :: t as l -> if n = 0 then x :: l else h :: insert_at x (n - 1) t;;
val insert_at : 'a -> int -> 'a list -> 'a list = <fun>
Create a List Containing All Integers Within a Given Range
If first argument is greater than second, produce a list in decreasing order.
# range 4 9;;
- : int list = [4; 5; 6; 7; 8; 9]
# let range a b =
let rec aux a b =
if a > b then [] else a :: aux (a + 1) b
in
if a > b then List.rev (aux b a) else aux a b;;
val range : int -> int -> int list = <fun>
A tail recursive implementation:
# let range a b =
let rec aux acc high low =
if high >= low then
aux (high :: acc) (high - 1) low
else acc
in
if a < b then aux [] b a else List.rev (aux [] a b);;
val range : int -> int -> int list = <fun>
Extract a Given Number of Randomly Selected Elements From a List
The selected items shall be returned in a list. We use the Random
module but and initialise it with Random.init 0 at the start of
the function for reproducibility and validate the solution. To make the function truly random, however,
one should remove the call to Random.init 0
# rand_select ["a"; "b"; "c"; "d"; "e"; "f"; "g"; "h"] 3;;
- : string list = ["e"; "c"; "g"]
# let rand_select list n =
Random.init 0;
let rec extract acc n = function
| [] -> raise Not_found
| h :: t -> if n = 0 then (h, acc @ t) else extract (h :: acc) (n - 1) t
in
let extract_rand list len =
extract [] (Random.int len) list
in
let rec aux n acc list len =
if n = 0 then acc else
let picked, rest = extract_rand list len in
aux (n - 1) (picked :: acc) rest (len - 1)
in
let len = List.length list in
aux (min n len) [] list len;;
val rand_select : 'a list -> int -> 'a list = <fun>
Lotto: Draw N Different Random Numbers From the Set 1..M
Draw N different random numbers from the set 1..M.
The selected numbers shall be returned in a list.
# lotto_select 6 49;;
- : int list = [20; 28; 45; 16; 24; 38]
# (* [range] and [rand_select] defined in problems above *)
let lotto_select n m = rand_select (range 1 m) n;;
val lotto_select : int -> int -> int list = <fun>
Generate a Random Permutation of the Elements of a List
Generate a random permutation of the elements of a list.
# permutation ["a"; "b"; "c"; "d"; "e"; "f"];;
- : string list = ["c"; "d"; "f"; "e"; "b"; "a"]
# let permutation list =
let rec extract acc n = function
| [] -> raise Not_found
| h :: t -> if n = 0 then (h, acc @ t) else extract (h :: acc) (n - 1) t
in
let extract_rand list len =
extract [] (Random.int len) list
in
let rec aux acc list len =
if len = 0 then acc else
let picked, rest = extract_rand list len in
aux (picked :: acc) rest (len - 1)
in
aux [] list (List.length list);;
val permutation : 'a list -> 'a list = <fun>
Generate the Combinations of K Distinct Objects Chosen From the N Elements of a List
Generate the combinations of K distinct objects chosen from the N elements of a list.
In how many ways can a committee of 3 be chosen from a group of 12 people? We all know that there are C(12,3) = 220 possibilities (C(N,K) denotes the well-known binomial coefficients). For pure mathematicians, this result may be great. But we want to really generate all the possibilities in a list.
# extract 2 ["a"; "b"; "c"; "d"];;
- : string list list =
[["a"; "b"]; ["a"; "c"]; ["a"; "d"]; ["b"; "c"]; ["b"; "d"]; ["c"; "d"]]
# let rec extract k list =
if k <= 0 then [[]]
else match list with
| [] -> []
| h :: tl ->
let with_h = List.map (fun l -> h :: l) (extract (k - 1) tl) in
let without_h = extract k tl in
with_h @ without_h;;
val extract : int -> 'a list -> 'a list list = <fun>
Group the Elements of a Set Into Disjoint Subsets
Group the elements of a set into disjoint subsets
- In how many ways can a group of 9 people work in 3 disjoint subgroups of 2, 3 and 4 persons? Write a function that generates all the possibilities and returns them in a list.
- Generalize the above function in a way that we can specify a list of group sizes and the function will return a list of groups.
# group ["a"; "b"; "c"; "d"] [2; 1];;
- : string list list list =
[[["a"; "b"]; ["c"]]; [["a"; "c"]; ["b"]]; [["b"; "c"]; ["a"]];
[["a"; "b"]; ["d"]]; [["a"; "c"]; ["d"]]; [["b"; "c"]; ["d"]];
[["a"; "d"]; ["b"]]; [["b"; "d"]; ["a"]]; [["a"; "d"]; ["c"]];
[["b"; "d"]; ["c"]]; [["c"; "d"]; ["a"]]; [["c"; "d"]; ["b"]]]
# (* This implementation is less streamlined than the one-extraction
version, because more work is done on the lists after each
transform to prepend the actual items. The end result is cleaner
in terms of code, though. *)
let group list sizes =
let initial = List.map (fun size -> size, []) sizes in
(* The core of the function. Prepend accepts a list of groups,
each with the number of items that should be added, and
prepends the item to every group that can support it, thus
turning [1,a ; 2,b ; 0,c] into [ [0,x::a ; 2,b ; 0,c ];
[1,a ; 1,x::b ; 0,c]; [ 1,a ; 2,b ; 0,c ]]
Again, in the prolog language (for which these questions are
originally intended), this function is a whole lot simpler. *)
let prepend p list =
let emit l acc = l :: acc in
let rec aux emit acc = function
| [] -> emit [] acc
| (n, l) as h :: t ->
let acc = if n > 0 then emit ((n - 1, p :: l) :: t) acc
else acc in
aux (fun l acc -> emit (h :: l) acc) acc t
in
aux emit [] list
in
let rec aux = function
| [] -> [initial]
| h :: t -> List.concat_map (prepend h) (aux t)
in
let all = aux list in
(* Don't forget to eliminate all group sets that have non-full
groups *)
let complete = List.filter (List.for_all (fun (x, _) -> x = 0)) all in
List.map (List.map snd) complete;;
val group : 'a list -> int list -> 'a list list list = <fun>
Sorting a List of Lists According to Length of Sublists
Sorting a list of lists according to length of sublists.
-
We suppose that a list contains elements that are lists themselves. The objective is to sort the elements of this list according to their length. E.g. short lists first, longer lists later, or vice versa.
-
Again, we suppose that a list contains elements that are lists themselves. But this time the objective is to sort the elements of this list according to their length frequency; i.e., in the default, where sorting is done ascendingly, lists with rare lengths are placed first, others with a more frequent length come later.
# length_sort [["a"; "b"; "c"]; ["d"; "e"]; ["f"; "g"; "h"]; ["d"; "e"];
["i"; "j"; "k"; "l"]; ["m"; "n"]; ["o"]];;
- : string list list =
[["o"]; ["d"; "e"]; ["d"; "e"]; ["m"; "n"]; ["a"; "b"; "c"]; ["f"; "g"; "h"];
["i"; "j"; "k"; "l"]]
# frequency_sort [["a"; "b"; "c"]; ["d"; "e"]; ["f"; "g"; "h"]; ["d"; "e"];
["i"; "j"; "k"; "l"]; ["m"; "n"]; ["o"]];;
- : string list list =
[["i"; "j"; "k"; "l"]; ["o"]; ["a"; "b"; "c"]; ["f"; "g"; "h"]; ["d"; "e"];
["d"; "e"]; ["m"; "n"]]
(* We might not be allowed to use built-in List.sort, so here's an
eight-line implementation of insertion sort — O(n²) time
complexity. *)
let rec insert cmp e = function
| [] -> [e]
| h :: t as l -> if cmp e h <= 0 then e :: l else h :: insert cmp e t
let rec sort cmp = function
| [] -> []
| h :: t -> insert cmp h (sort cmp t)
(* Sorting according to length : prepend length, sort, remove length *)
let length_sort lists =
let lists = List.map (fun list -> List.length list, list) lists in
let lists = sort (fun a b -> compare (fst a) (fst b)) lists in
List.map snd lists
;;
(* Sorting according to length frequency : prepend frequency, sort,
remove frequency. Frequencies are extracted by sorting lengths
and applying RLE to count occurrences of each length (see problem
"Run-length encoding of a list.") *)
let rle list =
let rec aux count acc = function
| [] -> [] (* Can only be reached if original list is empty *)
| [x] -> (x, count + 1) :: acc
| a :: (b :: _ as t) ->
if a = b then aux (count + 1) acc t
else aux 0 ((a, count + 1) :: acc) t in
aux 0 [] list
let frequency_sort lists =
let lengths = List.map List.length lists in
let freq = rle (sort compare lengths) in
let by_freq =
List.map (fun list -> List.assoc (List.length list) freq , list) lists in
let sorted = sort (fun a b -> compare (fst a) (fst b)) by_freq in
List.map snd sorted
Determine Whether a Given Integer Number Is Prime
Determine whether a given integer number is prime.
# not (is_prime 1);;
- : bool = true
# is_prime 7;;
- : bool = true
# not (is_prime 12);;
- : bool = true
Recall that d divides n if and only if n mod d = 0. This is a naive
solution. See the Sieve of
Eratosthenes for a
more clever one.
# let is_prime n =
let n = abs n in
let rec is_not_divisor d =
d * d > n || (n mod d <> 0 && is_not_divisor (d + 1)) in
n > 1 && is_not_divisor 2;;
val is_prime : int -> bool = <fun>
Determine the Greatest Common Divisor of Two Positive Integer Numbers
Determine the greatest common divisor of two positive integer numbers.
Use Euclid's algorithm.
# gcd 13 27;;
- : int = 1
# gcd 20536 7826;;
- : int = 2
# let rec gcd a b =
if b = 0 then a else gcd b (a mod b);;
val gcd : int -> int -> int = <fun>
Determine Whether Two Positive Integer Numbers Are Coprime
Determine whether two positive integer numbers are coprime.
Two numbers are coprime if their greatest common divisor equals 1.
# coprime 13 27;;
- : bool = true
# not (coprime 20536 7826);;
- : bool = true
# (* [gcd] is defined in the previous question *)
let coprime a b = gcd a b = 1;;
val coprime : int -> int -> bool = <fun>
Calculate Euler's Totient Function Φ(m)
Euler's so-called totient function φ(m) is defined as the number of positive integers r (1 ≤ r < m) that are coprime to m. We let φ(1) = 1.
Find out what the value of φ(m) is if m is a prime number. Euler's totient function plays an important role in one of the most widely used public key cryptography methods (RSA). In this exercise you should use the most primitive method to calculate this function (there are smarter ways that we shall discuss later).
# phi 10;;
- : int = 4
# (* [coprime] is defined in the previous question *)
let phi n =
let rec count_coprime acc d =
if d < n then
count_coprime (if coprime n d then acc + 1 else acc) (d + 1)
else acc
in
if n = 1 then 1 else count_coprime 0 1;;
val phi : int -> int = <fun>
Determine the Prime Factors of a Given Positive Integer
Construct a flat list containing the prime factors in ascending order.
# factors 315;;
- : int list = [3; 3; 5; 7]
# (* Recall that d divides n iff [n mod d = 0] *)
let factors n =
let rec aux d n =
if n = 1 then [] else
if n mod d = 0 then d :: aux d (n / d) else aux (d + 1) n
in
aux 2 n;;
val factors : int -> int list = <fun>
Determine the Prime Factors of a Given Positive Integer (2)
Construct a list containing the prime factors and their multiplicity.
Hint: The problem is similar to problem Run-length encoding of a list (direct solution).
# factors 315;;
- : (int * int) list = [(3, 2); (5, 1); (7, 1)]
# let factors n =
let rec aux d n =
if n = 1 then [] else
if n mod d = 0 then
match aux d (n / d) with
| (h, n) :: t when h = d -> (h, n + 1) :: t
| l -> (d, 1) :: l
else aux (d + 1) n
in
aux 2 n;;
val factors : int -> (int * int) list = <fun>
Calculate Euler's Totient Function Φ(m) (Improved)
See problem "Calculate Euler's totient function φ(m)" for
the definition of Euler's totient function. If the list of the prime
factors of a number m is known in the form of the previous problem then
the function phi(m) can be efficiently calculated as follows: Let
[(p1, m1); (p2, m2); (p3, m3); ...] be the list of prime factors
(and their multiplicities) of a given number m. Then φ(m) can be
calculated with the following formula:
φ(m) = (p1 - 1) × p1m1 - 1 × (p2 - 1) × p2m2 - 1 × (p3 - 1) × p3m3 - 1 × ⋯
# phi_improved 10;;
- : int = 4
# phi_improved 13;;
- : int = 12
(* Naive power function. *)
let rec pow n p = if p < 1 then 1 else n * pow n (p - 1)
(* [factors] is defined in the previous question. *)
let phi_improved n =
let rec aux acc = function
| [] -> acc
| (p, m) :: t -> aux ((p - 1) * pow p (m - 1) * acc) t
in
aux 1 (factors n)
Compare the Two Methods of Calculating Euler's Totient Function
Use the solutions of problems "Calculate Euler's totient function φ(m)" and "Calculate Euler's totient function φ(m) (improved)" to compare the algorithms. Take the number of logical inferences as a measure for efficiency. Try to calculate φ(10090) as an example.
timeit phi 10090
# (* Naive [timeit] function. It requires the [Unix] module to be loaded. *)
let timeit f a =
let t0 = Unix.gettimeofday() in
ignore (f a);
let t1 = Unix.gettimeofday() in
t1 -. t0;;
val timeit : ('a -> 'b) -> 'a -> float = <fun>
A List of Prime Numbers
Given a range of integers by its lower and upper limit, construct a list of all prime numbers in that range.
# List.length (all_primes 2 7920);;
- : int = 1000
# let is_prime n =
let n = max n (-n) in
let rec is_not_divisor d =
d * d > n || (n mod d <> 0 && is_not_divisor (d + 1))
in
is_not_divisor 2
let rec all_primes a b =
if a > b then [] else
let rest = all_primes (a + 1) b in
if is_prime a then a :: rest else rest;;
val is_prime : int -> bool = <fun>
val all_primes : int -> int -> int list = <fun>
Goldbach's Conjecture
Goldbach's conjecture says that every positive even number greater than 2 is the sum of two prime numbers. Example: 28 = 5 + 23. It is one of the most famous facts in number theory that has not been proved to be correct in the general case. It has been numerically confirmed up to very large numbers. Write a function to find the two prime numbers that sum up to a given even integer.
# goldbach 28;;
- : int * int = (5, 23)
# (* [is_prime] is defined in the previous solution *)
let goldbach n =
let rec aux d =
if is_prime d && is_prime (n - d) then (d, n - d)
else aux (d + 1)
in
aux 2;;
val goldbach : int -> int * int = <fun>
A List of Goldbach Compositions
Given a range of integers by its lower and upper limit, print a list of all even numbers and their Goldbach composition.
In most cases, if an even number is written as the sum of two prime numbers, one of them is very small. Very rarely, the primes are both bigger than say 50. Try to find out how many such cases there are in the range 2..3000.
# goldbach_list 9 20;;
- : (int * (int * int)) list =
[(10, (3, 7)); (12, (5, 7)); (14, (3, 11)); (16, (3, 13)); (18, (5, 13));
(20, (3, 17))]
# (* [goldbach] is defined in the previous question. *)
let rec goldbach_list a b =
if a > b then [] else
if a mod 2 = 1 then goldbach_list (a + 1) b
else (a, goldbach a) :: goldbach_list (a + 2) b
let goldbach_limit a b lim =
List.filter (fun (_, (a, b)) -> a > lim && b > lim) (goldbach_list a b);;
val goldbach_list : int -> int -> (int * (int * int)) list = <fun>
val goldbach_limit : int -> int -> int -> (int * (int * int)) list = <fun>
Truth Tables for Logical Expressions (2 Variables)
Let us define a small "language" for boolean expressions containing variables:
# type bool_expr =
| Var of string
| Not of bool_expr
| And of bool_expr * bool_expr
| Or of bool_expr * bool_expr;;
type bool_expr =
Var of string
| Not of bool_expr
| And of bool_expr * bool_expr
| Or of bool_expr * bool_expr
A logical expression in two variables can then be written in prefix
notation. For example, (a ∨ b) ∧ (a ∧ b) is written:
# And (Or (Var "a", Var "b"), And (Var "a", Var "b"));;
- : bool_expr = And (Or (Var "a", Var "b"), And (Var "a", Var "b"))
Define a function, table2 which returns the truth table of a given
logical expression in two variables (specified as arguments). The return
value must be a list of triples containing
(value_of_a, value_of_b, value_of_expr).
# table2 "a" "b" (And (Var "a", Or (Var "a", Var "b")));;
- : (bool * bool * bool) list =
[(true, true, true); (true, false, true); (false, true, false);
(false, false, false)]
# let rec eval2 a val_a b val_b = function
| Var x -> if x = a then val_a
else if x = b then val_b
else failwith "The expression contains an invalid variable"
| Not e -> not (eval2 a val_a b val_b e)
| And(e1, e2) -> eval2 a val_a b val_b e1 && eval2 a val_a b val_b e2
| Or(e1, e2) -> eval2 a val_a b val_b e1 || eval2 a val_a b val_b e2
let table2 a b expr =
[(true, true, eval2 a true b true expr);
(true, false, eval2 a true b false expr);
(false, true, eval2 a false b true expr);
(false, false, eval2 a false b false expr)];;
val eval2 : string -> bool -> string -> bool -> bool_expr -> bool = <fun>
val table2 : string -> string -> bool_expr -> (bool * bool * bool) list =
<fun>
Truth Tables for Logical Expressions
Generalize the previous problem in such a way that the logical
expression may contain any number of logical variables. Define table
in a way that table variables expr returns the truth table for the
expression expr, which contains the logical variables enumerated in
variables.
# table ["a"; "b"] (And (Var "a", Or (Var "a", Var "b")));;
- : ((string * bool) list * bool) list =
[([("a", true); ("b", true)], true); ([("a", true); ("b", false)], true);
([("a", false); ("b", true)], false); ([("a", false); ("b", false)], false)]
# (* [val_vars] is an associative list containing the truth value of
each variable. For efficiency, a Map or a Hashtlb should be
preferred. *)
let rec eval val_vars = function
| Var x -> List.assoc x val_vars
| Not e -> not (eval val_vars e)
| And(e1, e2) -> eval val_vars e1 && eval val_vars e2
| Or(e1, e2) -> eval val_vars e1 || eval val_vars e2
(* Again, this is an easy and short implementation rather than an
efficient one. *)
let rec table_make val_vars vars expr =
match vars with
| [] -> [(List.rev val_vars, eval val_vars expr)]
| v :: tl ->
table_make ((v, true) :: val_vars) tl expr
@ table_make ((v, false) :: val_vars) tl expr
let table vars expr = table_make [] vars expr;;
val eval : (string * bool) list -> bool_expr -> bool = <fun>
val table_make :
(string * bool) list ->
string list -> bool_expr -> ((string * bool) list * bool) list = <fun>
val table : string list -> bool_expr -> ((string * bool) list * bool) list =
<fun>
Gray Code
An n-bit Gray code is a sequence of n-bit strings constructed according to certain rules. For example,
n = 1: C(1) = ['0', '1'].
n = 2: C(2) = ['00', '01', '11', '10'].
n = 3: C(3) = ['000', '001', '011', '010', '110', '111', '101', '100'].
Find out the construction rules and write a function with the following
specification: gray n returns the n-bit Gray code.
# gray 1;;
- : string list = ["0"; "1"]
# gray 2;;
- : string list = ["00"; "01"; "11"; "10"]
# gray 3;;
- : string list = ["000"; "001"; "011"; "010"; "110"; "111"; "101"; "100"]
# let gray n =
let rec gray_next_level k l =
if k < n then
(* This is the core part of the Gray code construction.
* first_half is reversed and has a "0" attached to every element.
* Second part is reversed (it must be reversed for correct gray code).
* Every element has "1" attached to the front.*)
let (first_half,second_half) =
List.fold_left (fun (acc1,acc2) x ->
(("0" ^ x) :: acc1, ("1" ^ x) :: acc2)) ([], []) l
in
(* List.rev_append turns first_half around and attaches it to second_half.
* The result is the modified first_half in correct order attached to
* the second_half modified in reversed order.*)
gray_next_level (k + 1) (List.rev_append first_half second_half)
else l
in
gray_next_level 1 ["0"; "1"];;
val gray : int -> string list = <fun>
Huffman Code
First of all, consult a good book on discrete mathematics or algorithms for a detailed description of Huffman codes (you can start with the Wikipedia page)!
We consider a set of symbols with their frequencies.
For example, if the alphabet is "a",..., "f"
(represented as the positions 0,...5) and
respective frequencies are 45, 13, 12, 16, 9, 5:
# let fs = [("a", 45); ("b", 13); ("c", 12); ("d", 16);
("e", 9); ("f", 5)];;
val fs : (string * int) list =
[("a", 45); ("b", 13); ("c", 12); ("d", 16); ("e", 9); ("f", 5)]
Our objective is to construct the
Huffman code c word for all symbols s. In our example, the result could
be
hs = [("a", "0"); ("b", "101"); ("c", "100"); ("d", "111"); ("e", "1101"); ("f", "1100")]
(or hs = [("a", "1");...]). The task shall be performed by the function
huffman defined as follows: huffman(fs) returns the Huffman code
table for the frequency table fs
# huffman fs;;
- : (string * string) list =
[("a", "0"); ("c", "100"); ("b", "101"); ("f", "1100"); ("e", "1101");
("d", "111")]
# (* Simple priority queue where the priorities are integers 0..100.
The node with the lowest probability comes first. *)
module Pq = struct
type 'a t = {data: 'a list array; mutable first: int}
let make() = {data = Array.make 101 []; first = 101}
let add q p x =
q.data.(p) <- x :: q.data.(p); q.first <- min p q.first
let get_min q =
if q.first = 101 then None else
match q.data.(q.first) with
| [] -> assert false
| x :: tl ->
let p = q.first in
q.data.(q.first) <- tl;
while q.first < 101 && q.data.(q.first) = [] do
q.first <- q.first + 1
done;
Some(p, x)
end
type tree =
| Leaf of string
| Node of tree * tree
let rec huffman_tree q =
match Pq.get_min q, Pq.get_min q with
| Some(p1, t1), Some(p2, t2) -> Pq.add q (p1 + p2) (Node(t1, t2));
huffman_tree q
| Some(_, t), None | None, Some(_, t) -> t
| None, None -> assert false
(* Build the prefix-free binary code from the tree *)
let rec prefixes_of_tree prefix = function
| Leaf s -> [(s, prefix)]
| Node(t0, t1) -> prefixes_of_tree (prefix ^ "0") t0
@ prefixes_of_tree (prefix ^ "1") t1
let huffman fs =
if List.fold_left (fun s (_, p) -> s + p) 0 fs <> 100 then
failwith "huffman: sum of weights must be 100";
let q = Pq.make () in
List.iter (fun (s, f) -> Pq.add q f (Leaf s)) fs;
prefixes_of_tree "" (huffman_tree q);;
module Pq :
sig
type 'a t = { data : 'a list array; mutable first : int; }
val make : unit -> 'a t
val add : 'a t -> int -> 'a -> unit
val get_min : 'a t -> (int * 'a) option
end
type tree = Leaf of string | Node of tree * tree
val huffman_tree : tree Pq.t -> tree = <fun>
val prefixes_of_tree : string -> tree -> (string * string) list = <fun>
val huffman : (string * int) list -> (string * string) list = <fun>
Construct Completely Balanced Binary Trees
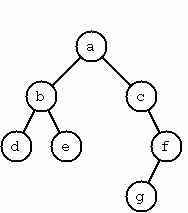
A binary tree is either empty or it is composed of a root element and two successors, which are binary trees themselves.
In OCaml, one can define a new type binary_tree that carries an
arbitrary value of type 'a (thus is polymorphic) at each node.
# type 'a binary_tree =
| Empty
| Node of 'a * 'a binary_tree * 'a binary_tree;;
type 'a binary_tree = Empty | Node of 'a * 'a binary_tree * 'a binary_tree
An example of tree carrying char data is:
# let example_tree =
Node ('a', Node ('b', Node ('d', Empty, Empty), Node ('e', Empty, Empty)),
Node ('c', Empty, Node ('f', Node ('g', Empty, Empty), Empty)));;
val example_tree : char binary_tree =
Node ('a', Node ('b', Node ('d', Empty, Empty), Node ('e', Empty, Empty)),
Node ('c', Empty, Node ('f', Node ('g', Empty, Empty), Empty)))
In OCaml, the strict type discipline guarantees that, if you get a
value of type binary_tree, then it must have been created with the two
constructors Empty and Node.
In a completely balanced binary tree, the following property holds for every node: The number of nodes in its left subtree and the number of nodes in its right subtree are almost equal, which means their difference is not greater than one.
Write a function cbal_tree to construct completely balanced binary
trees for a given number of nodes. The function should generate all
solutions via backtracking. Put the letter 'x' as information into all
nodes of the tree.
# cbal_tree 4;;
- : char binary_tree/2 list =
[Node ('x', Node ('x', Empty, Empty),
Node ('x', Node ('x', Empty, Empty), Empty));
Node ('x', Node ('x', Empty, Empty),
Node ('x', Empty, Node ('x', Empty, Empty)));
Node ('x', Node ('x', Node ('x', Empty, Empty), Empty),
Node ('x', Empty, Empty));
Node ('x', Node ('x', Empty, Node ('x', Empty, Empty)),
Node ('x', Empty, Empty))]
# (* Build all trees with given [left] and [right] subtrees. *)
let add_trees_with left right all =
let add_right_tree all l =
List.fold_left (fun a r -> Node ('x', l, r) :: a) all right in
List.fold_left add_right_tree all left
let rec cbal_tree n =
if n = 0 then [Empty]
else if n mod 2 = 1 then
let t = cbal_tree (n / 2) in
add_trees_with t t []
else (* n even: n-1 nodes for the left & right subtrees altogether. *)
let t1 = cbal_tree (n / 2 - 1) in
let t2 = cbal_tree (n / 2) in
add_trees_with t1 t2 (add_trees_with t2 t1 []);;
val add_trees_with :
char binary_tree list ->
char binary_tree list -> char binary_tree list -> char binary_tree list =
<fun>
val cbal_tree : int -> char binary_tree list = <fun>
Symmetric Binary Trees
Let us call a binary tree symmetric if you can draw a vertical line
through the root node and then the right subtree is the mirror image of
the left subtree. Write a function is_symmetric to check whether a
given binary tree is symmetric.
Hint: Write a function is_mirror first to check whether one tree
is the mirror image of another. We are only interested in the
structure, not in the contents of the nodes.
# let rec is_mirror t1 t2 =
match t1, t2 with
| Empty, Empty -> true
| Node(_, l1, r1), Node(_, l2, r2) ->
is_mirror l1 r2 && is_mirror r1 l2
| _ -> false
let is_symmetric = function
| Empty -> true
| Node(_, l, r) -> is_mirror l r;;
val is_mirror : 'a binary_tree -> 'b binary_tree -> bool = <fun>
val is_symmetric : 'a binary_tree -> bool = <fun>
Binary Search Trees (Dictionaries)
Construct a binary search tree from a list of integer numbers.
# construct [3; 2; 5; 7; 1];;
- : int binary_tree =
Node (3, Node (2, Node (1, Empty, Empty), Empty),
Node (5, Empty, Node (7, Empty, Empty)))
Then use this function to test the solution of the previous problem.
# is_symmetric (construct [5; 3; 18; 1; 4; 12; 21]);;
- : bool = true
# not (is_symmetric (construct [3; 2; 5; 7; 4]));;
- : bool = true
# let rec insert tree x = match tree with
| Empty -> Node (x, Empty, Empty)
| Node (y, l, r) ->
if x = y then tree
else if x < y then Node (y, insert l x, r)
else Node (y, l, insert r x)
let construct l = List.fold_left insert Empty l;;
val insert : 'a binary_tree -> 'a -> 'a binary_tree = <fun>
val construct : 'a list -> 'a binary_tree = <fun>
Generate-and-Test Paradigm
Apply the generate-and-test paradigm to construct all symmetric, completely balanced binary trees with a given number of nodes.
# sym_cbal_trees 5;;
- : char binary_tree list =
[Node ('x', Node ('x', Node ('x', Empty, Empty), Empty),
Node ('x', Empty, Node ('x', Empty, Empty)));
Node ('x', Node ('x', Empty, Node ('x', Empty, Empty)),
Node ('x', Node ('x', Empty, Empty), Empty))]
How many such trees are there with 57 nodes? Investigate about how many solutions there are for a given number of nodes? What if the number is even? Write an appropriate function.
# List.length (sym_cbal_trees 57);;
- : int = 256
# let sym_cbal_trees n =
List.filter is_symmetric (cbal_tree n);;
val sym_cbal_trees : int -> char binary_tree list = <fun>
Construct Height-Balanced Binary Trees
In a height-balanced binary tree, the following property holds for every node: The height of its left subtree and the height of its right subtree are almost equal, which means their difference is not greater than one.
Write a function hbal_tree to construct height-balanced binary trees
for a given height. The function should generate all solutions via
backtracking. Put the letter 'x' as information into all nodes of the
tree.
# let t = hbal_tree 3;;
val t : char binary_tree list =
[Node ('x', Node ('x', Empty, Node ('x', Empty, Empty)),
Node ('x', Empty, Node ('x', Empty, Empty)));
Node ('x', Node ('x', Empty, Node ('x', Empty, Empty)),
Node ('x', Node ('x', Empty, Empty), Empty));
Node ('x', Node ('x', Empty, Node ('x', Empty, Empty)),
Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)));
Node ('x', Node ('x', Node ('x', Empty, Empty), Empty),
Node ('x', Empty, Node ('x', Empty, Empty)));
Node ('x', Node ('x', Node ('x', Empty, Empty), Empty),
Node ('x', Node ('x', Empty, Empty), Empty));
Node ('x', Node ('x', Node ('x', Empty, Empty), Empty),
Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)));
Node ('x', Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)),
Node ('x', Empty, Node ('x', Empty, Empty)));
Node ('x', Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)),
Node ('x', Node ('x', Empty, Empty), Empty));
Node ('x', Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)),
Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)));
Node ('x', Node ('x', Empty, Node ('x', Empty, Empty)),
Node ('x', Empty, Empty));
Node ('x', Node ('x', Node ('x', Empty, Empty), Empty),
Node ('x', Empty, Empty));
Node ('x', Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)),
Node ('x', Empty, Empty));
Node ('x', Node ('x', Empty, Empty),
Node ('x', Empty, Node ('x', Empty, Empty)));
Node ('x', Node ('x', Empty, Empty),
Node ('x', Node ('x', Empty, Empty), Empty));
Node ('x', Node ('x', Empty, Empty),
Node ('x', Node ('x', Empty, Empty), Node ('x', Empty, Empty)))]
The function add_trees_with is defined in the solution of
Construct completely balanced binary trees.
# let rec hbal_tree n =
if n = 0 then [Empty]
else if n = 1 then [Node ('x', Empty, Empty)]
else
(* [add_trees_with left right trees] is defined in a question above. *)
let t1 = hbal_tree (n - 1)
and t2 = hbal_tree (n - 2) in
add_trees_with t1 t1 (add_trees_with t1 t2 (add_trees_with t2 t1 []));;
val hbal_tree : int -> char binary_tree list = <fun>
Construct Height-Balanced Binary Trees With a Given Number of Nodes
Consider a height-balanced binary tree of height h. What is the
maximum number of nodes it can contain? Clearly,
max_nodes = 2h - 1.
# let max_nodes h = 1 lsl h - 1;;
val max_nodes : int -> int = <fun>
Minimum of nodes
However, what is the minimum number min_nodes? This question is more
difficult. Try to find a recursive statement and turn it into a function
min_nodes defined as follows: min_nodes h returns the minimum number
of nodes in a height-balanced binary tree of height h.
Minimum height
On the other hand, we might ask: what are the minimum (resp. maximum)
height H a
height-balanced binary tree with N nodes can have?
min_height (resp. max_height n) returns
the minimum (resp. maximum) height of a height-balanced binary tree
with n nodes.
Constructing trees
Now, we can attack the main problem: construct all the height-balanced
binary trees with a given number of nodes. hbal_tree_nodes n returns a
list of all height-balanced binary tree with n nodes.
Find out how many height-balanced trees exist for n = 15.
# List.length (hbal_tree_nodes 15);;
- : int = 1553
Minimum of nodes
The following solution comes directly from translating the question.
# let rec min_nodes h =
if h <= 0 then 0
else if h = 1 then 1
else min_nodes (h - 1) + min_nodes (h - 2) + 1;;
val min_nodes : int -> int = <fun>
It is not the more efficient one however. One should use the last two values as the state to avoid the double recursion.
# let rec min_nodes_loop m0 m1 h =
if h <= 1 then m1
else min_nodes_loop m1 (m1 + m0 + 1) (h - 1)
let min_nodes h =
if h <= 0 then 0 else min_nodes_loop 0 1 h;;
val min_nodes_loop : int -> int -> int -> int = <fun>
val min_nodes : int -> int = <fun>
It is not difficult to show that min_nodes h = Fh+2 - 1,
where (Fn) is the
Fibonacci sequence.
Minimum height
Inverting the formula max_nodes = 2h - 1, one directly
find that Hₘᵢₙ(n) = ⌈log₂(n+1)⌉ which is readily implemented:
# let min_height n = int_of_float (ceil (log (float(n + 1)) /. log 2.));;
val min_height : int -> int = <fun>
Let us give a proof that the formula for Hₘᵢₙ is valid. First, if h
= min_height n, there exists a height-balanced tree of height h
with n nodes. Thus 2ʰ - 1 = max_nodes h ≥ n i.e., h ≥ log₂(n+1).
To establish equality for Hₘᵢₙ(n), one has to show that, for any n,
there exists a height-balanced tree with height Hₘᵢₙ(n). This is
due to the relation Hₘᵢₙ(n) = 1 + Hₘᵢₙ(n/2) where n/2 is the integer
division. For n odd, this is readily proved — so one can build a
tree with a top node and two sub-trees with n/2 nodes of height
Hₘᵢₙ(n) - 1. For n even, the same proof works if one first remarks
that, in that case, ⌈log₂(n+2)⌉ = ⌈log₂(n+1)⌉ — use log₂(n+1) ≤ h ∈
ℕ ⇔ 2ʰ ≥ n + 1 and the fact that 2ʰ is even for that. This allows
to have a sub-tree with n/2 nodes. For the other sub-tree with
n/2-1 nodes, one has to establish that Hₘᵢₙ(n/2-1) ≥ Hₘᵢₙ(n) - 2
which is easy because, if h = Hₘᵢₙ(n/2-1), then h+2 ≥ log₂(2n) ≥
log₂(n+1).
The above function is not the best one however. Indeed, not every 64 bits integer can be represented exactly as a floating point number. Here is one that only uses integer operations:
# let rec ceil_log2_loop log plus1 n =
if n = 1 then if plus1 then log + 1 else log
else ceil_log2_loop (log + 1) (plus1 || n land 1 <> 0) (n / 2)
let ceil_log2 n = ceil_log2_loop 0 false n;;
val ceil_log2_loop : int -> bool -> int -> int = <fun>
val ceil_log2 : int -> int = <fun>
This algorithm is still not the fastest however. See for example the Hacker's Delight, section 5-3 (and 11-4).
Following the same idea as above, if h = max_height n, then one
easily deduces that min_nodes h ≤ n < min_nodes(h+1). This
yields the following code:
# let rec max_height_search h n =
if min_nodes h <= n then max_height_search (h + 1) n else h - 1
let max_height n = max_height_search 0 n;;
val max_height_search : int -> int -> int = <fun>
val max_height : int -> int = <fun>
Of course, since min_nodes is computed recursively, there is no
need to recompute everything to go from min_nodes h to
min_nodes(h+1):
# let rec max_height_search h m_h m_h1 n =
if m_h <= n then max_height_search (h + 1) m_h1 (m_h1 + m_h + 1) n else h - 1
let max_height n = max_height_search 0 0 1 n;;
val max_height_search : int -> int -> int -> int -> int = <fun>
val max_height : int -> int = <fun>
Constructing trees
First, we define some convenience functions fold_range that folds
a function f on the range n0...n1 i.e., it computes
f (... f (f (f init n0) (n0+1)) (n0+2) ...) n1. You can think it
as performing the assignment init ← f init n for n = n0,..., n1
except that there is no mutable variable in the code.
# let rec fold_range ~f ~init n0 n1 =
if n0 > n1 then init else fold_range ~f ~init:(f init n0) (n0 + 1) n1;;
val fold_range : f:('a -> int -> 'a) -> init:'a -> int -> int -> 'a = <fun>
When constructing trees, there is an obvious symmetry: if one swaps
the left and right sub-trees of a balanced tree, we still have a
balanced tree. The following function returns all trees in trees
together with their permutation.
# let rec add_swap_left_right trees =
List.fold_left (fun a n -> match n with
| Node (v, t1, t2) -> Node (v, t2, t1) :: a
| Empty -> a) trees trees;;
val add_swap_left_right : 'a binary_tree list -> 'a binary_tree list = <fun>
Finally we generate all trees recursively, using a priori the bounds computed above. It could be further optimized but our aim is to straightforwardly express the idea.
# let rec hbal_tree_nodes_height h n =
assert(min_nodes h <= n && n <= max_nodes h);
if h = 0 then [Empty]
else
let acc = add_hbal_tree_node [] (h - 1) (h - 2) n in
let acc = add_swap_left_right acc in
add_hbal_tree_node acc (h - 1) (h - 1) n
and add_hbal_tree_node l h1 h2 n =
let min_n1 = max (min_nodes h1) (n - 1 - max_nodes h2) in
let max_n1 = min (max_nodes h1) (n - 1 - min_nodes h2) in
fold_range min_n1 max_n1 ~init:l ~f:(fun l n1 ->
let t1 = hbal_tree_nodes_height h1 n1 in
let t2 = hbal_tree_nodes_height h2 (n - 1 - n1) in
List.fold_left (fun l t1 ->
List.fold_left (fun l t2 -> Node ('x', t1, t2) :: l) l t2) l t1
)
let hbal_tree_nodes n =
fold_range (min_height n) (max_height n) ~init:[] ~f:(fun l h ->
List.rev_append (hbal_tree_nodes_height h n) l);;
val hbal_tree_nodes_height : int -> int -> char binary_tree list = <fun>
val add_hbal_tree_node :
char binary_tree list -> int -> int -> int -> char binary_tree list = <fun>
val hbal_tree_nodes : int -> char binary_tree list = <fun>
Count the Leaves of a Binary Tree
A leaf is a node with no successors. Write a function count_leaves to
count them.
# count_leaves Empty;;
- : int = 0
# let rec count_leaves = function
| Empty -> 0
| Node (_, Empty, Empty) -> 1
| Node (_, l, r) -> count_leaves l + count_leaves r;;
val count_leaves : 'a binary_tree -> int = <fun>
Collect the Leaves of a Binary Tree in a List
A leaf is a node with no successors. Write a function leaves to
collect them in a list.
# leaves Empty;;
- : 'a list = []
# (* Having an accumulator acc prevents using inefficient List.append.
* Every Leaf will be pushed directly into accumulator.
* Not tail-recursive, but that is no problem since we have a binary tree and
* and stack depth is logarithmic. *)
let leaves t =
let rec leaves_aux t acc = match t with
| Empty -> acc
| Node (x, Empty, Empty) -> x :: acc
| Node (x, l, r) -> leaves_aux l (leaves_aux r acc)
in
leaves_aux t [];;
val leaves : 'a binary_tree -> 'a list = <fun>
Collect the Internal Nodes of a Binary Tree in a List
An internal node of a binary tree has either one or two non-empty
successors. Write a function internals to collect them in a list.
# internals (Node ('a', Empty, Empty));;
- : char list = []
# (* Having an accumulator acc prevents using inefficient List.append.
* Every internal node will be pushed directly into accumulator.
* Not tail-recursive, but that is no problem since we have a binary tree and
* and stack depth is logarithmic. *)
let internals t =
let rec internals_aux t acc = match t with
| Empty -> acc
| Node (x, Empty, Empty) -> acc
| Node (x, l, r) -> internals_aux l (x :: internals_aux r acc)
in
internals_aux t [];;
val internals : 'a binary_tree -> 'a list = <fun>
Collect the Nodes at a Given Level in a List
A node of a binary tree is at level N if the path from the root to the
node has length N-1. The root node is at level 1. Write a function
at_level t l to collect all nodes of the tree t at level l in a
list.
# let example_tree =
Node ('a', Node ('b', Node ('d', Empty, Empty), Node ('e', Empty, Empty)),
Node ('c', Empty, Node ('f', Node ('g', Empty, Empty), Empty)));;
val example_tree : char binary_tree =
Node ('a', Node ('b', Node ('d', Empty, Empty), Node ('e', Empty, Empty)),
Node ('c', Empty, Node ('f', Node ('g', Empty, Empty), Empty)))
# at_level example_tree 2;;
- : char list = ['b'; 'c']
Using at_level it is easy to construct a function levelorder which
creates the level-order sequence of the nodes. However, there are more
efficient ways to do that.
# (* Having an accumulator acc prevents using inefficient List.append.
* Every node at level N will be pushed directly into accumulator.
* Not tail-recursive, but that is no problem since we have a binary tree and
* and stack depth is logarithmic. *)
let at_level t level =
let rec at_level_aux t acc counter = match t with
| Empty -> acc
| Node (x, l, r) ->
if counter=level then
x :: acc
else
at_level_aux l (at_level_aux r acc (counter + 1)) (counter + 1)
in
at_level_aux t [] 1;;
val at_level : 'a binary_tree -> int -> 'a list = <fun>
Construct a Complete Binary Tree
A complete binary tree with height H is defined as follows: The levels 1,2,3,...,H-1 contain the maximum number of nodes (i.e 2i-1 at the level i, note that we start counting the levels from 1 at the root). In level H, which may contain less than the maximum possible number of nodes, all the nodes are "left-adjusted". This means that in a levelorder tree traversal all internal nodes come first, the leaves come second, and empty successors (the nil's which are not really nodes!) come last.
Particularly, complete binary trees are used as data structures (or addressing schemes) for heaps.
We can assign an address number to each node in a complete binary tree
by enumerating the nodes in levelorder, starting at the root with
number 1. In doing so, we realize that for every node X with address A
the following property holds: The address of X's left and right
successors are 2*A and 2*A+1, respectively, supposed the successors do
exist. This fact can be used to elegantly construct a complete binary
tree structure. Write a function is_complete_binary_tree with the
following specification: is_complete_binary_tree n t returns true
iff t is a complete binary tree with n nodes.
# complete_binary_tree [1; 2; 3; 4; 5; 6];;
- : int binary_tree =
Node (1, Node (2, Node (4, Empty, Empty), Node (5, Empty, Empty)),
Node (3, Node (6, Empty, Empty), Empty))
# let rec split_n lst acc n = match (n, lst) with
| (0, _) -> (List.rev acc, lst)
| (_, []) -> (List.rev acc, [])
| (_, h :: t) -> split_n t (h :: acc) (n-1)
let rec myflatten p c =
match (p, c) with
| (p, []) -> List.map (fun x -> Node (x, Empty, Empty)) p
| (x :: t, [y]) -> Node (x, y, Empty) :: myflatten t []
| (ph :: pt, x :: y :: t) -> (Node (ph, x, y)) :: myflatten pt t
| _ -> invalid_arg "myflatten"
let complete_binary_tree = function
| [] -> Empty
| lst ->
let rec aux l = function
| [] -> []
| lst -> let p, c = split_n lst [] (1 lsl l) in
myflatten p (aux (l + 1) c)
in
List.hd (aux 0 lst);;
val split_n : 'a list -> 'a list -> int -> 'a list * 'a list = <fun>
val myflatten : 'a list -> 'a binary_tree list -> 'a binary_tree list = <fun>
val complete_binary_tree : 'a list -> 'a binary_tree = <fun>
Layout a Binary Tree (1)
As a preparation for drawing the tree, a layout algorithm is required to determine the position of each node in a rectangular grid. Several layout methods are conceivable, one of them is shown in the illustration.
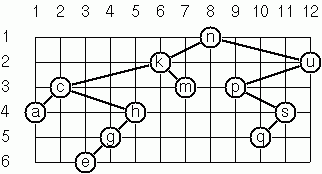
In this layout strategy, the position of a node v is obtained by the following two rules:
- x(v) is equal to the position of the node v in the inorder sequence;
- y(v) is equal to the depth of the node v in the tree.
In order to store the position of the nodes, we will enrich the value
at each node with the position (x,y).
The tree pictured above is
# let example_layout_tree =
let leaf x = Node (x, Empty, Empty) in
Node ('n', Node ('k', Node ('c', leaf 'a',
Node ('h', Node ('g', leaf 'e', Empty), Empty)),
leaf 'm'),
Node ('u', Node ('p', Empty, Node ('s', leaf 'q', Empty)), Empty));;
val example_layout_tree : char binary_tree =
Node ('n',
Node ('k',
Node ('c', Node ('a', Empty, Empty),
Node ('h', Node ('g', Node ('e', Empty, Empty), Empty), Empty)),
Node ('m', Empty, Empty)),
Node ('u', Node ('p', Empty, Node ('s', Node ('q', Empty, Empty), Empty)),
Empty))
# layout_binary_tree_1 example_layout_tree;;
- : (char * int * int) binary_tree =
Node (('n', 8, 1),
Node (('k', 6, 2),
Node (('c', 2, 3), Node (('a', 1, 4), Empty, Empty),
Node (('h', 5, 4),
Node (('g', 4, 5), Node (('e', 3, 6), Empty, Empty), Empty), Empty)),
Node (('m', 7, 3), Empty, Empty)),
Node (('u', 12, 2),
Node (('p', 9, 3), Empty,
Node (('s', 11, 4), Node (('q', 10, 5), Empty, Empty), Empty)),
Empty))
# let layout_binary_tree_1 t =
let rec layout depth x_left = function
(* This function returns a pair: the laid out tree and the first
* free x location *)
| Empty -> (Empty, x_left)
| Node (v,l,r) ->
let (l', l_x_max) = layout (depth + 1) x_left l in
let (r', r_x_max) = layout (depth + 1) (l_x_max + 1) r in
(Node ((v, l_x_max, depth), l', r'), r_x_max)
in
fst (layout 1 1 t);;
val layout_binary_tree_1 : 'a binary_tree -> ('a * int * int) binary_tree =
<fun>
Layout a Binary Tree (2)
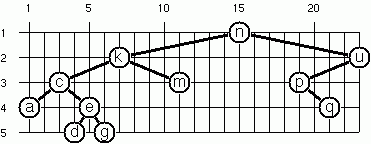
An alternative layout method is depicted in this illustration. Find out the rules and write the corresponding OCaml function.
Hint: On a given level, the horizontal distance between neighbouring nodes is constant.
The tree shown is
# let example_layout_tree =
let leaf x = Node (x, Empty, Empty) in
Node ('n', Node ('k', Node ('c', leaf 'a',
Node ('e', leaf 'd', leaf 'g')),
leaf 'm'),
Node ('u', Node ('p', Empty, leaf 'q'), Empty));;
val example_layout_tree : char binary_tree =
Node ('n',
Node ('k',
Node ('c', Node ('a', Empty, Empty),
Node ('e', Node ('d', Empty, Empty), Node ('g', Empty, Empty))),
Node ('m', Empty, Empty)),
Node ('u', Node ('p', Empty, Node ('q', Empty, Empty)), Empty))
# layout_binary_tree_2 example_layout_tree ;;
- : (char * int * int) binary_tree =
Node (('n', 15, 1),
Node (('k', 7, 2),
Node (('c', 3, 3), Node (('a', 1, 4), Empty, Empty),
Node (('e', 5, 4), Node (('d', 4, 5), Empty, Empty),
Node (('g', 6, 5), Empty, Empty))),
Node (('m', 11, 3), Empty, Empty)),
Node (('u', 23, 2),
Node (('p', 19, 3), Empty, Node (('q', 21, 4), Empty, Empty)), Empty))
# let layout_binary_tree_2 t =
let rec height = function
| Empty -> 0
| Node (_, l, r) -> 1 + max (height l) (height r) in
let tree_height = height t in
let rec find_missing_left depth = function
| Empty -> tree_height - depth
| Node (_, l, _) -> find_missing_left (depth + 1) l in
let translate_dst = 1 lsl (find_missing_left 0 t) - 1 in
(* remember than 1 lsl a = 2ᵃ *)
let rec layout depth x_root = function
| Empty -> Empty
| Node (x, l, r) ->
let spacing = 1 lsl (tree_height - depth - 1) in
let l' = layout (depth + 1) (x_root - spacing) l
and r' = layout (depth + 1) (x_root + spacing) r in
Node((x, x_root, depth), l',r') in
layout 1 ((1 lsl (tree_height - 1)) - translate_dst) t;;
val layout_binary_tree_2 : 'a binary_tree -> ('a * int * int) binary_tree =
<fun>
Layout a Binary Tree (3)
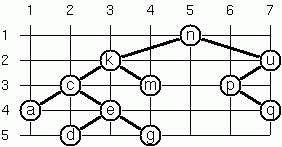
Yet another layout strategy is shown in the above illustration. The method yields a very compact layout while maintaining a certain symmetry in every node. Find out the rules and write the corresponding predicate.
Hint: Consider the horizontal distance between a node and its successor nodes. How tight can you pack together two subtrees to construct the combined binary tree? This is a difficult problem. Don't give up too early!
# let example_layout_tree =
let leaf x = Node (x, Empty, Empty) in
Node ('n', Node ('k', Node ('c', leaf 'a',
Node ('h', Node ('g', leaf 'e', Empty), Empty)),
leaf 'm'),
Node ('u', Node ('p', Empty, Node ('s', leaf 'q', Empty)), Empty));;
val example_layout_tree : char binary_tree =
Node ('n',
Node ('k',
Node ('c', Node ('a', Empty, Empty),
Node ('h', Node ('g', Node ('e', Empty, Empty), Empty), Empty)),
Node ('m', Empty, Empty)),
Node ('u', Node ('p', Empty, Node ('s', Node ('q', Empty, Empty), Empty)),
Empty))
# layout_binary_tree_3 example_layout_tree ;;
- : (char * int * int) binary_tree =
Node (('n', 5, 1),
Node (('k', 3, 2),
Node (('c', 2, 3), Node (('a', 1, 4), Empty, Empty),
Node (('h', 3, 4),
Node (('g', 2, 5), Node (('e', 1, 6), Empty, Empty), Empty), Empty)),
Node (('m', 4, 3), Empty, Empty)),
Node (('u', 7, 2),
Node (('p', 6, 3), Empty,
Node (('s', 7, 4), Node (('q', 6, 5), Empty, Empty), Empty)),
Empty))
Which layout do you like most?
In order to pack the tree tightly, the layout function will return in addition to the layout of the tree the left and right profiles of the tree, that is lists of offsets relative to the position of the root node of the tree.
# let layout_binary_tree_3 =
let rec translate_x d = function
| Empty -> Empty
| Node ((v, x, y), l, r) ->
Node ((v, x + d, y), translate_x d l, translate_x d r) in
(* Distance between a left subtree given by its right profile [lr]
and a right subtree given by its left profile [rl]. *)
let rec dist lr rl = match lr, rl with
| lrx :: ltl, rlx :: rtl -> max (lrx - rlx) (dist ltl rtl)
| [], _ | _, [] -> 0 in
let rec merge_profiles p1 p2 = match p1, p2 with
| x1 :: tl1, _ :: tl2 -> x1 :: merge_profiles tl1 tl2
| [], _ -> p2
| _, [] -> p1 in
let rec layout depth = function
| Empty -> ([], Empty, [])
| Node (v, l, r) ->
let (ll, l', lr) = layout (depth + 1) l in
let (rl, r', rr) = layout (depth + 1) r in
let d = 1 + dist lr rl / 2 in
let ll = List.map (fun x -> x - d) ll
and lr = List.map (fun x -> x - d) lr
and rl = List.map ((+) d) rl
and rr = List.map ((+) d) rr in
(0 :: merge_profiles ll rl,
Node((v, 0, depth), translate_x (-d) l', translate_x d r'),
0 :: merge_profiles rr lr) in
fun t -> let (l, t', _) = layout 1 t in
let x_min = List.fold_left min 0 l in
translate_x (1 - x_min) t';;
val layout_binary_tree_3 : 'a binary_tree -> ('a * int * int) binary_tree =
<fun>
A String Representation of Binary Trees

Somebody represents binary trees as strings of the following type (see
example): "a(b(d,e),c(,f(g,)))".
- Write an OCaml function
string_of_treewhich generates this string representation, if the tree is given as usual (asEmptyorNode(x,l,r)term). Then write a functiontree_of_stringwhich does this inverse; i.e. given the string representation, construct the tree in the usual form. Finally, combine the two predicates in a single functiontree_stringwhich can be used in both directions. - Write the same predicate
tree_stringusing difference lists and a single predicatetree_dlistwhich does the conversion between a tree and a difference list in both directions.
For simplicity, suppose the information in the nodes is a single letter and there are no spaces in the string.
# let example_layout_tree =
let leaf x = Node (x, Empty, Empty) in
(Node ('a', Node ('b', leaf 'd', leaf 'e'),
Node ('c', Empty, Node ('f', leaf 'g', Empty))));;
val example_layout_tree : char binary_tree =
Node ('a', Node ('b', Node ('d', Empty, Empty), Node ('e', Empty, Empty)),
Node ('c', Empty, Node ('f', Node ('g', Empty, Empty), Empty)))
A simple solution is:
# let rec string_of_tree = function
| Empty -> ""
| Node(data, l, r) ->
let data = String.make 1 data in
match l, r with
| Empty, Empty -> data
| _, _ -> data ^ "(" ^ (string_of_tree l)
^ "," ^ (string_of_tree r) ^ ")";;
val string_of_tree : char binary_tree -> string = <fun>
One can also use a buffer to allocate a lot less memory:
# let rec buffer_add_tree buf = function
| Empty -> ()
| Node (data, l, r) ->
Buffer.add_char buf data;
match l, r with
| Empty, Empty -> ()
| _, _ -> Buffer.add_char buf '(';
buffer_add_tree buf l;
Buffer.add_char buf ',';
buffer_add_tree buf r;
Buffer.add_char buf ')'
let string_of_tree t =
let buf = Buffer.create 128 in
buffer_add_tree buf t;
Buffer.contents buf;;
val buffer_add_tree : Buffer.t -> char binary_tree -> unit = <fun>
val string_of_tree : char binary_tree -> string = <fun>
For the reverse conversion, we assume that the string is well formed and do not deal with error reporting.
# let tree_of_string =
let rec make ofs s =
if ofs >= String.length s || s.[ofs] = ',' || s.[ofs] = ')' then
(Empty, ofs)
else
let v = s.[ofs] in
if ofs + 1 < String.length s && s.[ofs + 1] = '(' then
let l, ofs = make (ofs + 2) s in (* skip "v(" *)
let r, ofs = make (ofs + 1) s in (* skip "," *)
(Node (v, l, r), ofs + 1) (* skip ")" *)
else (Node (v, Empty, Empty), ofs + 1)
in
fun s -> fst (make 0 s);;
val tree_of_string : string -> char binary_tree = <fun>
Preorder and Inorder Sequences of Binary Trees
We consider binary trees with nodes that are identified by single lower-case letters, as in the example of the previous problem.
- Write functions
preorderandinorderthat construct the preorder and inorder sequence of a given binary tree, respectively. The results should be atoms, e.g. 'abdecfg' for the preorder sequence of the example in the previous problem. - Can you use
preorderfrom problem part 1 in the reverse direction; i.e. given a preorder sequence, construct a corresponding tree? If not, make the necessary arrangements. - If both the preorder sequence and the inorder sequence of the nodes
of a binary tree are given, then the tree is determined
unambiguously. Write a function
pre_in_treethat does the job. - Solve problems 1 to 3 using
difference lists.
Cool! Use the
function
timeit(defined in problem “Compare the two methods of calculating Euler's totient function.”) to compare the solutions.
What happens if the same character appears in more than one node. Try
for instance pre_in_tree "aba" "baa".
# preorder (Node (1, Node (2, Empty, Empty), Empty));;
- : int list = [1; 2]
We use lists to represent the result. Note that preorder and inorder can be made more efficient by avoiding list concatenations.
# let rec preorder = function
| Empty -> []
| Node (v, l, r) -> v :: (preorder l @ preorder r)
let rec inorder = function
| Empty -> []
| Node (v, l, r) -> inorder l @ (v :: inorder r)
let rec split_pre_in p i x accp acci = match (p, i) with
| [], [] -> (List.rev accp, List.rev acci), ([], [])
| h1 :: t1, h2 :: t2 ->
if x = h2 then
(List.tl (List.rev (h1 :: accp)), t1),
(List.rev (List.tl (h2 :: acci)), t2)
else
split_pre_in t1 t2 x (h1 :: accp) (h2 :: acci)
| _ -> assert false
let rec pre_in_tree p i = match (p, i) with
| [], [] -> Empty
| (h1 :: t1), (h2 :: t2) ->
let (lp, rp), (li, ri) = split_pre_in p i h1 [] [] in
Node (h1, pre_in_tree lp li, pre_in_tree rp ri)
| _ -> invalid_arg "pre_in_tree";;
val preorder : 'a binary_tree -> 'a list = <fun>
val inorder : 'a binary_tree -> 'a list = <fun>
val split_pre_in :
'a list ->
'a list ->
'a -> 'a list -> 'a list -> ('a list * 'a list) * ('a list * 'a list) =
<fun>
val pre_in_tree : 'a list -> 'a list -> 'a binary_tree = <fun>
Solution using difference lists.
(* solution pending *)
Dotstring Representation of Binary Trees
We consider again binary trees with nodes that are identified by single
lower-case letters, as in the example of problem “A string
representation of binary trees”. Such a tree can be
represented by the preorder sequence of its nodes in which dots (.) are
inserted where an empty subtree (nil) is encountered during the tree
traversal. For example, the tree shown in problem “A string
representation of binary trees” is represented as
'abd..e..c.fg...'. First, try to establish a syntax (BNF or syntax
diagrams) and then write a function tree_dotstring which does the
conversion in both directions. Use difference lists.
(* solution pending *)
Tree Construction From a Node String
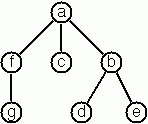
A multiway tree is composed of a root element and a (possibly empty) set of successors which are multiway trees themselves. A multiway tree is never empty. The set of successor trees is sometimes called a forest.
To represent multiway trees, we will use the following type which is a direct translation of the definition:
# type 'a mult_tree = T of 'a * 'a mult_tree list;;
type 'a mult_tree = T of 'a * 'a mult_tree list
The example tree depicted opposite is therefore represented by the following OCaml expression:
# T ('a', [T ('f', [T ('g', [])]); T ('c', []); T ('b', [T ('d', []); T ('e', [])])]);;
- : char mult_tree =
T ('a',
[T ('f', [T ('g', [])]); T ('c', []); T ('b', [T ('d', []); T ('e', [])])])
We suppose that the nodes of a multiway tree contain single characters.
In the depth-first order sequence of its nodes, a special character ^
has been inserted whenever, during the tree traversal, the move is a
backtrack to the previous level.
By this rule, the tree in the figure opposite is represented as:
afg^^c^bd^e^^^.
Write functions string_of_tree : char mult_tree -> string to construct
the string representing the tree and
tree_of_string : string -> char mult_tree to construct the tree when
the string is given.
# let t = T ('a', [T ('f', [T ('g', [])]); T ('c', []);
T ('b', [T ('d', []); T ('e', [])])]);;
val t : char mult_tree =
T ('a',
[T ('f', [T ('g', [])]); T ('c', []); T ('b', [T ('d', []); T ('e', [])])])
# (* We could build the final string by string concatenation but
this is expensive due to the number of operations. We use a
buffer instead. *)
let rec add_string_of_tree buf (T (c, sub)) =
Buffer.add_char buf c;
List.iter (add_string_of_tree buf) sub;
Buffer.add_char buf '^';;
val add_string_of_tree : Buffer.t -> char mult_tree -> unit = <fun>
# let string_of_tree t =
let buf = Buffer.create 128 in
add_string_of_tree buf t;
Buffer.contents buf;;
val string_of_tree : char mult_tree -> string = <fun>
# let tree_of_string s =
let rec parse_node chars =
match chars with
| [] -> failwith "Unexpected end of input (expecting node)"
| c :: rest ->
let (children, rest') = parse_children rest in
(T (c, children), rest')
and parse_children chars =
match chars with
| [] -> failwith "Unexpected end of input (expecting ^)"
| '^' :: rest -> ([], rest)
| _ ->
let (child, rest') = parse_node chars in
let (siblings, rest'') = parse_children rest' in
(child :: siblings, rest'')
in
let (tree, remaining) = parse_node (List.of_seq (String.to_seq s)) in
match remaining with
| [] -> tree
| _ -> failwith "Extra input after tree";;
val tree_of_string : string -> char mult_tree = <fun>
Count the Nodes of a Multiway Tree
# count_nodes (T ('a', [T ('f', []) ]));;
- : int = 2
# let rec count_nodes (T (_, sub)) =
List.fold_left (fun n t -> n + count_nodes t) 1 sub;;
val count_nodes : 'a mult_tree -> int = <fun>
Determine the Internal Path Length of a Tree
We define the internal path length of a multiway tree as the total sum
of the path lengths from the root to all nodes of the tree. By this
definition, the tree t in the figure of the previous problem has an
internal path length of 9. Write a function ipl tree that returns the
internal path length of tree.
# ipl t;;
- : int = 9
# let rec ipl_sub len (T(_, sub)) =
(* [len] is the distance of the current node to the root. Add the
distance of all sub-nodes. *)
List.fold_left (fun sum t -> sum + ipl_sub (len + 1) t) len sub
let ipl t = ipl_sub 0 t;;
val ipl_sub : int -> 'a mult_tree -> int = <fun>
val ipl : 'a mult_tree -> int = <fun>
Construct the Bottom-Up Order Sequence of the Tree Nodes
Write a function bottom_up t which constructs the bottom-up sequence
of the nodes of the multiway tree t.
# bottom_up (T ('a', [T ('b', [])]));;
- : char list = ['b'; 'a']
# bottom_up t;;
- : char list = ['g'; 'f'; 'c'; 'd'; 'e'; 'b'; 'a']
# let rec prepend_bottom_up (T (c, sub)) l =
List.fold_right (fun t l -> prepend_bottom_up t l) sub (c :: l)
let bottom_up t = prepend_bottom_up t [];;
val prepend_bottom_up : 'a mult_tree -> 'a list -> 'a list = <fun>
val bottom_up : 'a mult_tree -> 'a list = <fun>
Lisp-Like Tree Representation
There is a particular notation for multiway trees in Lisp. The picture shows how multiway tree structures are represented in Lisp.
Note that in the "lispy" notation a node with successors (children) in
the tree is always the first element in a list, followed by its
children. The "lispy" representation of a multiway tree is a sequence of
atoms and parentheses '(' and ')'. This is very close to the way trees
are represented in OCaml, except that no constructor T is used. Write
a function lispy : char mult_tree -> string that returns the
lispy notation of the tree.
# lispy (T ('a', []));;
- : string = "a"
# lispy (T ('a', [T ('b', [])]));;
- : string = "(a b)"
# lispy t;;
- : string = "(a (f g) c (b d e))"
# let rec add_lispy buf = function
| T(c, []) -> Buffer.add_char buf c
| T(c, sub) ->
Buffer.add_char buf '(';
Buffer.add_char buf c;
List.iter (fun t -> Buffer.add_char buf ' '; add_lispy buf t) sub;
Buffer.add_char buf ')'
let lispy t =
let buf = Buffer.create 128 in
add_lispy buf t;
Buffer.contents buf;;
val add_lispy : Buffer.t -> char mult_tree -> unit = <fun>
val lispy : char mult_tree -> string = <fun>
Conversions
A graph is defined as a set of nodes and a set of edges, where each edge is a pair of different nodes.
There are several ways to represent graphs in OCaml.
- One method is to list all edges, an edge being a pair of nodes. In this form, the graph depicted above is represented as the following expression:
# [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')];;
- : (char * char) list =
[('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]
We call this edge-clause form. Obviously, isolated nodes cannot be represented.
- Another method is to represent the whole graph as one data object. According to the definition of the graph as a pair of two sets (nodes and edges), we may use the following OCaml type:
# type 'a graph_term = {nodes : 'a list; edges : ('a * 'a) list};;
type 'a graph_term = { nodes : 'a list; edges : ('a * 'a) list; }
Then, the above example graph is represented by:
# let example_graph =
{nodes = ['b'; 'c'; 'd'; 'f'; 'g'; 'h'; 'k'];
edges = [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]};;
val example_graph : char graph_term =
{nodes = ['b'; 'c'; 'd'; 'f'; 'g'; 'h'; 'k'];
edges = [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]}
We call this graph-term form. Note, that the lists are kept
sorted, they are really sets, without duplicated elements. Each edge
appears only once in the edge list; i.e. an edge from a node x to
another node y is represented as (x, y), the couple (y, x) is not
present. The graph-term form is our default representation. You
may want to define a similar type using sets instead of lists.
- A third representation method is to associate with each node the set of nodes that are adjacent to that node. We call this the adjacency-list form. In our example:
let adjacency_example = ['b', ['c'; 'f'];
'c', ['b'; 'f'];
'd', [];
'f', ['b'; 'c'; 'k'];
'g', ['h'];
'h', ['g'];
'k', ['f']
];;
val adjacency_example : (char * char list) list =
[('b', ['c'; 'f']); ('c', ['b'; 'f']); ('d', []); ('f', ['b'; 'c'; 'k']);
('g', ['h']); ('h', ['g']); ('k', ['f'])]
- The representations we introduced so far are well suited for automated processing, but their syntax is not very user-friendly. Typing the terms by hand is cumbersome and error-prone. We can define a more compact and "human-friendly" notation as follows: A graph (with char labelled nodes) is represented by a string of atoms and terms of the type X-Y. The atoms stand for isolated nodes, the X-Y terms describe edges. If an X appears as an endpoint of an edge, it is automatically defined as a node. Our example could be written as:
# "b-c f-c g-h d f-b k-f h-g";;
- : string = "b-c f-c g-h d f-b k-f h-g"
We call this the human-friendly form. As the example shows, the
list does not have to be sorted and may even contain the same edge
multiple times. Notice the isolated node d.
Write functions to convert between the different graph representations. With these functions, all representations are equivalent; i.e. for the following problems you can always pick freely the most convenient form. This problem is not particularly difficult, but it's a lot of work to deal with all the special cases.
(* example pending *)
Path From One Node to Another One
Write a function paths g a b that returns all acyclic path p from
node a to node b ≠ a in the graph g. The function should return
the list of all paths via backtracking.
# let example_graph =
{nodes = ['b'; 'c'; 'd'; 'f'; 'g'; 'h'; 'k'];
edges = [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]};;
val example_graph : char graph_term =
{nodes = ['b'; 'c'; 'd'; 'f'; 'g'; 'h'; 'k'];
edges = [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]}
# paths example_graph 'f' 'b';;
- : char list list = [['f'; 'c'; 'b']; ['f'; 'b']]
# (* The datastructures used here are far from the most efficient ones
but allow for a straightforward implementation. *)
(* Returns all neighbors satisfying the condition. *)
let neighbors g a cond =
let edge l (b, c) = if b = a && cond c then c :: l
else if c = a && cond b then b :: l
else l in
List.fold_left edge [] g.edges
let rec list_path g a to_b = match to_b with
| [] -> assert false (* [to_b] contains the path to [b]. *)
| a' :: _ ->
if a' = a then [to_b]
else
let n = neighbors g a' (fun c -> not (List.mem c to_b)) in
List.concat_map (fun c -> list_path g a (c :: to_b)) n
let paths g a b =
assert(a <> b);
list_path g a [b];;
val neighbors : 'a graph_term -> 'a -> ('a -> bool) -> 'a list = <fun>
val list_path : 'a graph_term -> 'a -> 'a list -> 'a list list = <fun>
val paths : 'a graph_term -> 'a -> 'a -> 'a list list = <fun>
Cycle From a Given Node
Write a functions cycle g a that returns a closed path (cycle) p
starting at a given node a in the graph g. The predicate should
return the list of all cycles via backtracking.
# let example_graph =
{nodes = ['b'; 'c'; 'd'; 'f'; 'g'; 'h'; 'k'];
edges = [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]};;
val example_graph : char graph_term =
{nodes = ['b'; 'c'; 'd'; 'f'; 'g'; 'h'; 'k'];
edges = [('h', 'g'); ('k', 'f'); ('f', 'b'); ('f', 'c'); ('c', 'b')]}
# cycles example_graph 'f';;
- : char list list =
[['f'; 'b'; 'c'; 'f']; ['f'; 'c'; 'f']; ['f'; 'c'; 'b'; 'f'];
['f'; 'b'; 'f']; ['f'; 'k'; 'f']]
# let cycles g a =
let n = neighbors g a (fun _ -> true) in
let p = List.concat_map (fun c -> list_path g a [c]) n in
List.map (fun p -> p @ [a]) p;;
val cycles : 'a graph_term -> 'a -> 'a list list = <fun>
Construct All Spanning Trees
Write a function s_tree g to construct (by backtracking) all spanning
trees of a given graph g.
With this predicate, find out how many spanning trees there are for the
graph depicted to the left. The data of this example graph can be found
in the test below. When you have a correct solution for the s_tree
function, use it to define two other useful functions: is_tree graph
and is_connected Graph. Both are five-minutes tasks!
# let g = {nodes = ['a'; 'b'; 'c'; 'd'; 'e'; 'f'; 'g'; 'h'];
edges = [('a', 'b'); ('a', 'd'); ('b', 'c'); ('b', 'e');
('c', 'e'); ('d', 'e'); ('d', 'f'); ('d', 'g');
('e', 'h'); ('f', 'g'); ('g', 'h')]};;
val g : char graph_term =
{nodes = ['a'; 'b'; 'c'; 'd'; 'e'; 'f'; 'g'; 'h'];
edges =
[('a', 'b'); ('a', 'd'); ('b', 'c'); ('b', 'e'); ('c', 'e'); ('d', 'e');
('d', 'f'); ('d', 'g'); ('e', 'h'); ('f', 'g'); ('g', 'h')]}
(* solution pending *);;
Construct the Minimal Spanning Tree
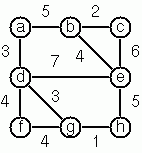
Write a function ms_tree graph to construct the minimal spanning tree
of a given labelled graph. A labelled graph will be represented as
follows:
# type ('a, 'b) labeled_graph = {nodes : 'a list;
labeled_edges : ('a * 'a * 'b) list};;
type ('a, 'b) labeled_graph = {
nodes : 'a list;
labeled_edges : ('a * 'a * 'b) list;
}
(Beware that from now on nodes and edges mask the previous fields of
the same name.)
Hint: Use the algorithm of Prim. A small modification of the solution of P83 does the trick. The data of the example graph to the right can be found below.
# let g = {nodes = ['a'; 'b'; 'c'; 'd'; 'e'; 'f'; 'g'; 'h'];
labeled_edges = [('a', 'b', 5); ('a', 'd', 3); ('b', 'c', 2);
('b', 'e', 4); ('c', 'e', 6); ('d', 'e', 7);
('d', 'f', 4); ('d', 'g', 3); ('e', 'h', 5);
('f', 'g', 4); ('g', 'h', 1)]};;
val g : (char, int) labeled_graph =
{nodes = ['a'; 'b'; 'c'; 'd'; 'e'; 'f'; 'g'; 'h'];
labeled_edges =
[('a', 'b', 5); ('a', 'd', 3); ('b', 'c', 2); ('b', 'e', 4);
('c', 'e', 6); ('d', 'e', 7); ('d', 'f', 4); ('d', 'g', 3);
('e', 'h', 5); ('f', 'g', 4); ('g', 'h', 1)]}
(* solution pending *);;
Graph Isomorphism
Two graphs G1(N1,E1) and G2(N2,E2) are isomorphic if there is a bijection f: N1 → N2 such that for any nodes X,Y of N1, X and Y are adjacent if and only if f(X) and f(Y) are adjacent.
Write a function that determines whether two graphs are isomorphic.
Hint: Use an open-ended list to represent the function f.
# let g = {nodes = [1; 2; 3; 4; 5; 6; 7; 8];
edges = [(1, 5); (1, 6); (1, 7); (2, 5); (2, 6); (2, 8); (3, 5);
(3, 7); (3, 8); (4, 6); (4, 7); (4, 8)]};;
val g : int graph_term =
{nodes = [1; 2; 3; 4; 5; 6; 7; 8];
edges =
[(1, 5); (1, 6); (1, 7); (2, 5); (2, 6); (2, 8); (3, 5); (3, 7);
(3, 8); (4, 6); (4, 7); (4, 8)]}
(* solution pending *);;
Node Degree and Graph Coloration
- Write a function
degree graph nodethat determines the degree of a given node. - Write a function that generates a list of all nodes of a graph sorted according to decreasing degree.
- Use Welsh-Powell's algorithm to paint the nodes of a graph in such a way that adjacent nodes have different colors.
(* example pending *);;
Depth-First Order Graph Traversal
Write a function that generates a depth-first order graph traversal sequence. The starting point should be specified, and the output should be a list of nodes that are reachable from this starting point (in depth-first order).
Specifically, the graph will be provided by its
adjacency-list representation
and you must create a module M with the following signature:
# module type GRAPH = sig
type node = char
type t
val of_adjacency : (node * node list) list -> t
val dfs_fold : t -> node -> ('a -> node -> 'a) -> 'a -> 'a
end;;
module type GRAPH =
sig
type node = char
type t
val of_adjacency : (node * node list) list -> t
val dfs_fold : t -> node -> ('a -> node -> 'a) -> 'a -> 'a
end
where M.dfs_fold g n f a applies f on the nodes of the graph
g in depth first order, starting with node n.
# let g = M.of_adjacency
['u', ['v'; 'x'];
'v', ['y'];
'w', ['z'; 'y'];
'x', ['v'];
'y', ['x'];
'z', ['z'];
];;
val g : M.t = <abstr>
In a depth-first search you fully explore the edges of the most recently discovered node v before 'backtracking' to explore edges leaving the node from which v was discovered. To do a depth-first search means keeping careful track of what vertices have been visited and when.
We compute timestamps for each vertex discovered in the search. A
discovered vertex has two timestamps associated with it : its
discovery time (in map d) and its finishing time (in map f) (a
vertex is finished when its adjacency list has been completely
examined). These timestamps are often useful in graph algorithms and
aid in reasoning about the behavior of depth-first search.
We color nodes during the search to help in the bookkeeping (map
color). All vertices of the graph are initially White. When a
vertex is discovered it is marked Gray and when it is finished, it
is marked Black.
If vertex v is discovered in the adjacency list of previously
discovered node u, this fact is recorded in the predecessor subgraph
(map pred).
# module M : GRAPH = struct
module Char_map = Map.Make (Char)
type node = char
type t = (node list) Char_map.t
let of_adjacency l =
List.fold_right (fun (x, y) -> Char_map.add x y) l Char_map.empty
type colors = White|Gray|Black
type 'a state = {
d : int Char_map.t; (*discovery time*)
f : int Char_map.t; (*finishing time*)
pred : char Char_map.t; (*predecessor*)
color : colors Char_map.t; (*vertex colors*)
acc : 'a; (*user specified type used by 'fold'*)
}
let dfs_fold g c fn acc =
let rec dfs_visit t u {d; f; pred; color; acc} =
let edge (t, state) v =
if Char_map.find v state.color = White then
dfs_visit t v {state with pred = Char_map.add v u state.pred}
else (t, state)
in
let t, {d; f; pred; color; acc} =
let t = t + 1 in
List.fold_left edge
(t, {d = Char_map.add u t d; f;
pred; color = Char_map.add u Gray color; acc = fn acc u})
(Char_map.find u g)
in
let t = t + 1 in
t , {d; f = Char_map.add u t f; pred;
color = Char_map.add u Black color; acc}
in
let v = List.fold_left (fun k (x, _) -> x :: k) []
(Char_map.bindings g) in
let initial_state=
{d = Char_map.empty;
f = Char_map.empty;
pred = Char_map.empty;
color = List.fold_right (fun x -> Char_map.add x White)
v Char_map.empty;
acc}
in
(snd (dfs_visit 0 c initial_state)).acc
end;;
module M : GRAPH
Connected Components
Write a predicate that splits a graph into its connected components.
(* example pending *);;
Bipartite Graphs
Write a predicate that finds out whether a given graph is bipartite.
(* example pending *);;
Generate K-Regular Simple Graphs With N Nodes
In a K-regular graph all nodes have a degree of K; i.e. the number of edges incident in each node is K. How many (non-isomorphic!) 3-regular graphs with 6 nodes are there?
See also the table of results.
(* example pending *);;
Eight Queens Problem
This is a classical problem in computer science. The objective is to place eight queens on a chessboard so that no two queens are attacking each other; i.e., no two queens are in the same row, the same column, or on the same diagonal.
Hint: Represent the positions of the queens as a list of numbers 1..N.
Example: [4; 2; 7; 3; 6; 8; 5; 1] means that the queen in the first column is
in row 4, the queen in the second column is in row 2, etc. Use the
generate-and-test paradigm.
# queens_positions 4;;
- : int list list = [[3; 1; 4; 2]; [2; 4; 1; 3]]
This is a brute force algorithm enumerating all possible solutions. For a deeper analysis, look for example to Wikipedia.
# let possible row col used_rows usedD1 usedD2 =
not (List.mem row used_rows
|| List.mem (row + col) usedD1
|| List.mem (row - col) usedD2)
let queens_positions n =
let rec aux row col used_rows usedD1 usedD2 =
if col > n then [List.rev used_rows]
else
(if row < n then aux (row + 1) col used_rows usedD1 usedD2
else [])
@ (if possible row col used_rows usedD1 usedD2 then
aux 1 (col + 1) (row :: used_rows) (row + col :: usedD1)
(row - col :: usedD2)
else [])
in aux 1 1 [] [] [];;
val possible : int -> int -> int list -> int list -> int list -> bool = <fun>
val queens_positions : int -> int list list = <fun>
Knight's Tour
Another famous problem is this one: How can a knight jump on an N×N chessboard in such a way that it visits every square exactly once?
Hint: Represent the squares by pairs of their coordinates (x,y),
where both x and y are integers between 1 and N. Define the function
jump n (x,y) that returns all coordinates (u,v) to which a
knight can jump from (x,y) to on a n×n chessboard. And finally,
represent the solution of our problem as a list knight positions (the
knight's tour).
(* example pending *);;
Von Koch's Conjecture
Several years ago I met a mathematician who was intrigued by a problem for which he didn't know a solution. His name was Von Koch, and I don't know whether the problem has been solved since.
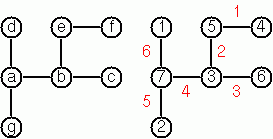
Anyway, the puzzle goes like this: Given a tree with N nodes (and hence N-1 edges). Find a way to enumerate the nodes from 1 to N and, accordingly, the edges from 1 to N-1 in such a way, that for each edge K the difference of its node numbers equals to K. The conjecture is that this is always possible.
For small trees the problem is easy to solve by hand. However, for larger trees, and 14 is already very large, it is extremely difficult to find a solution. And remember, we don't know for sure whether there is always a solution!
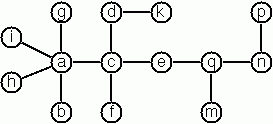
Write a function that calculates a numbering scheme for a given tree. What is the solution for the larger tree pictured here?
(* example pending *);;
An Arithmetic Puzzle
Given a list of integer numbers, find a correct way of inserting
arithmetic signs (operators) such that the result is a correct equation.
Example: With the list of numbers [2; 3; 5; 7; 11] we can form the
equations 2 - 3 + 5 + 7 = 11 or 2 = (3 * 5 + 7) / 11 (and ten others!).
(* example pending *);;
English Number Words
On financial documents, like cheques, numbers must sometimes be written
in full words. Example: 175 must be written as one-seven-five. Write a
function full_words to print (non-negative) integer numbers in full
words.
# full_words 175;;
- : string = "one-seven-five"
# let full_words =
let digit = [|"zero"; "one"; "two"; "three"; "four"; "five"; "six";
"seven"; "eight"; "nine"|] in
let rec words w n =
if n = 0 then (match w with [] -> [digit.(0)] | _ -> w)
else words (digit.(n mod 10) :: w) (n / 10)
in
fun n -> String.concat "-" (words [] n);;
val full_words : int -> string = <fun>
Syntax Checker
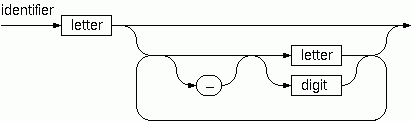
In a certain programming language (Ada) identifiers are defined by the
syntax diagram (railroad chart) opposite. Transform the syntax diagram
into a system of syntax diagrams which do not contain loops; i.e. which
are purely recursive. Using these modified diagrams, write a function
identifier : string -> bool that can check whether or not a given
string is a legal identifier.
# identifier "this-is-a-long-identifier";;
- : bool = true
# let identifier =
let is_letter c = 'a' <= c && c <= 'z' in
let is_letter_or_digit c = is_letter c || ('0' <= c && c <= '9') in
let rec is_valid s i not_after_dash =
if i < 0 then not_after_dash
else if is_letter_or_digit s.[i] then is_valid s (i - 1) true
else if s.[i] = '-' && not_after_dash then is_valid s (i - 1) false
else false in
fun s -> (
let n = String.length s in
n > 0 && is_letter s.[n - 1] && is_valid s (n - 2) true);;
val identifier : string -> bool = <fun>
Sudoku
Sudoku puzzles go like this:
Problem statement Solution
. . 4 | 8 . . | . 1 7 9 3 4 | 8 2 5 | 6 1 7
| | | |
6 7 . | 9 . . | . . . 6 7 2 | 9 1 4 | 8 5 3
| | | |
5 . 8 | . 3 . | . . 4 5 1 8 | 6 3 7 | 9 2 4
--------+---------+-------- --------+---------+--------
3 . . | 7 4 . | 1 . . 3 2 5 | 7 4 8 | 1 6 9
| | | |
. 6 9 | . . . | 7 8 . 4 6 9 | 1 5 3 | 7 8 2
| | | |
. . 1 | . 6 9 | . . 5 7 8 1 | 2 6 9 | 4 3 5
--------+---------+-------- --------+---------+--------
1 . . | . 8 . | 3 . 6 1 9 7 | 5 8 2 | 3 4 6
| | | |
. . . | . . 6 | . 9 1 8 5 3 | 4 7 6 | 2 9 1
| | | |
2 4 . | . . 1 | 5 . . 2 4 6 | 3 9 1 | 5 7 8
Every spot in the puzzle belongs to a (horizontal) row and a (vertical) column, as well as to one single 3x3 square (which we call "square" for short). At the beginning, some of the spots carry a single-digit number between 1 and 9. The problem is to fill the missing spots with digits in such a way that every number between 1 and 9 appears exactly once in each row, in each column, and in each square.
# (* The board representation is not imposed. Here "0" stands for "." *);;
A simple way of resolving this is to use brute force. The idea is to start filling with available values in each case and test if it works. When there is no available values, it means we made a mistake so we go back to the last choice we made, and try a different choice.
# open Printf
module Board = struct
type t = int array (* 9×9, row-major representation. A value of 0
means undecided. *)
let is_valid c = c >= 1
let get (b : t) (x, y) = b.(x + y * 9)
let get_as_string (b : t) pos =
let i = get b pos in
if is_valid i then string_of_int i else "."
let with_val (b : t) (x, y) v =
let b = Array.copy b in
b.(x + y * 9) <- v;
b
let of_list l : t =
let b = Array.make 81 0 in
List.iteri (fun y r -> List.iteri (fun x e ->
b.(x + y * 9) <- if e >= 0 && e <= 9 then e else 0) r) l;
b
let print b =
for y = 0 to 8 do
for x = 0 to 8 do
printf (if x = 0 then "%s" else if x mod 3 = 0 then " | %s"
else " %s") (get_as_string b (x, y))
done;
if y < 8 then
if y mod 3 = 2 then printf "\n--------+---------+--------\n"
else printf "\n | | \n"
else printf "\n"
done
let available b (x, y) =
let avail = Array.make 10 true in
for i = 0 to 8 do
avail.(get b (x, i)) <- false;
avail.(get b (i, y)) <- false;
done;
let sq_x = x - x mod 3 and sq_y = y - y mod 3 in
for x = sq_x to sq_x + 2 do
for y = sq_y to sq_y + 2 do
avail.(get b (x, y)) <- false;
done;
done;
let av = ref [] in
for i = 1 (* not 0 *) to 9 do if avail.(i) then av := i :: !av done;
!av
let next (x,y) = if x < 8 then (x + 1, y) else (0, y + 1)
(** Try to fill the undecided entries. *)
let rec fill b ((x, y) as pos) =
if y > 8 then Some b (* filled all entries *)
else if is_valid(get b pos) then fill b (next pos)
else match available b pos with
| [] -> None (* no solution *)
| l -> try_values b pos l
and try_values b pos = function
| v :: l ->
(match fill (with_val b pos v) (next pos) with
| Some _ as res -> res
| None -> try_values b pos l)
| [] -> None
end
let sudoku b = match Board.fill b (0, 0) with
| Some b -> b
| None -> failwith "sudoku: no solution";;
module Board :
sig
type t = int array
val is_valid : int -> bool
val get : t -> int * int -> int
val get_as_string : t -> int * int -> string
val with_val : t -> int * int -> int -> int array
val of_list : int list list -> t
val print : t -> unit
val available : t -> int * int -> int list
val next : int * int -> int * int
val fill : t -> int * int -> t option
val try_values : t -> int * int -> int list -> t option
end
val sudoku : Board.t -> Board.t = <fun>
Nonograms
Around 1994, a certain kind of puzzles was very popular in England. The "Sunday Telegraph" newspaper wrote: "Nonograms are puzzles from Japan and are currently published each week only in The Sunday Telegraph. Simply use your logic and skill to complete the grid and reveal a picture or diagram." As an OCaml programmer, you are in a better situation: you can have your computer do the work!
The puzzle goes like this: Essentially, each row and column of a rectangular bitmap is annotated with the respective lengths of its distinct strings of occupied cells. The person who solves the puzzle must complete the bitmap given only these lengths.
Problem statement: Solution:
|_|_|_|_|_|_|_|_| 3 |_|X|X|X|_|_|_|_| 3
|_|_|_|_|_|_|_|_| 2 1 |X|X|_|X|_|_|_|_| 2 1
|_|_|_|_|_|_|_|_| 3 2 |_|X|X|X|_|_|X|X| 3 2
|_|_|_|_|_|_|_|_| 2 2 |_|_|X|X|_|_|X|X| 2 2
|_|_|_|_|_|_|_|_| 6 |_|_|X|X|X|X|X|X| 6
|_|_|_|_|_|_|_|_| 1 5 |X|_|X|X|X|X|X|_| 1 5
|_|_|_|_|_|_|_|_| 6 |X|X|X|X|X|X|_|_| 6
|_|_|_|_|_|_|_|_| 1 |_|_|_|_|X|_|_|_| 1
|_|_|_|_|_|_|_|_| 2 |_|_|_|X|X|_|_|_| 2
1 3 1 7 5 3 4 3 1 3 1 7 5 3 4 3
2 1 5 1 2 1 5 1
For the example above, the problem can be stated as the two lists
[[3]; [2; 1]; [3; 2]; [2; 2]; [6]; [1; 5]; [6]; [1]; [2]] and
[[1; 2]; [3; 1]; [1; 5]; [7; 1]; [5]; [3]; [4]; [3]] which give the "solid"
lengths of the rows and columns, top-to-bottom and left-to-right,
respectively. Published puzzles are larger than this example, e.g.
25×20, and apparently always have unique solutions.
# solve [[3]; [2; 1]; [3; 2]; [2; 2]; [6]; [1; 5]; [6]; [1]; [2]]
[[1; 2]; [3; 1]; [1; 5]; [7; 1]; [5]; [3]; [4]; [3]];;
Brute force solution: construct boards trying all the fill possibilities for the columns given the prescribed patterns for them and reject the solution if it does not satisfy the row patterns.
# type element = Empty | X (* ensure we do not miss cases in patterns *);;
type element = Empty | X
You may want to look at more efficient algorithms and implement them so you can solve the following within reasonable time:
solve [[14]; [1; 1]; [7; 1]; [3; 3]; [2; 3; 2];
[2; 3; 2]; [1; 3; 6; 1; 1]; [1; 8; 2; 1]; [1; 4; 6; 1]; [1; 3; 2; 5; 1; 1];
[1; 5; 1]; [2; 2]; [2; 1; 1; 1; 2]; [6; 5; 3]; [12]]
[[7]; [2; 2]; [2; 2]; [2; 1; 1; 1; 1]; [1; 2; 4; 2];
[1; 1; 4; 2]; [1; 1; 2; 3]; [1; 1; 3; 2]; [1; 1; 1; 2; 2; 1]; [1; 1; 5; 1; 2];
[1; 1; 7; 2]; [1; 6; 3]; [1; 1; 3; 2]; [1; 4; 3]; [1; 3; 1];
[1; 2; 2]; [2; 1; 1; 1; 1]; [2; 2]; [2; 2]; [7]]
Crossword Puzzle
Given an empty (or almost empty) framework of a crossword puzzle and a set of words. The problem is to place the words into the framework.
The particular crossword puzzle is specified in a text file which first lists the words (one word per line) in an arbitrary order. Then, after an empty line, the crossword framework is defined. In this framework specification, an empty character location is represented by a dot (.). In order to make the solution easier, character locations can also contain predefined character values. The puzzle above is defined in the file p7_09a.dat, other examples are p7_09b.dat and p7_09d.dat. There is also an example of a puzzle (p7_09c.dat) which does not have a solution.
Words are strings (character lists) of at least two characters. A horizontal or vertical sequence of character places in the crossword puzzle framework is called a site. Our problem is to find a compatible way of placing words onto sites.
Hints:
- The problem is not easy. You will need some time to thoroughly understand it. So, don't give up too early! And remember that the objective is a clean solution, not just a quick-and-dirty hack!
- For efficiency reasons it is important, at least for larger puzzles, to sort the words and the sites in a particular order.
(* example pending *);;
Never-Ending Sequences
Lists are finite, meaning they always contain a finite number of elements. Sequences may be finite or infinite.
The goal of this exercise is to define a type 'a stream which only contains
infinite sequences. Using this type, define the following functions:
val hd : 'a stream -> 'a
(** Returns the first element of a stream *)
val tl : 'a stream -> 'a stream
(** Removes the first element of a stream *)
val take : int -> 'a stream -> 'a list
(** [take n seq] returns the n first values of [seq] *)
val unfold : ('a -> 'b * 'a) -> 'a -> 'b stream
(** Similar to Seq.unfold *)
val bang : 'a -> 'a stream
(** [bang x] produces an infinitely repeating sequence of [x] values. *)
val ints : int -> int stream
(* Similar to Seq.ints *)
val map : ('a -> 'b) -> 'a stream -> 'b stream
(** Similar to List.map and Seq.map *)
val filter: ('a -> bool) -> 'a stream -> 'a stream
(** Similar to List.filter and Seq.filter *)
val iter : ('a -> unit) -> 'a stream -> 'b
(** Similar to List.iter and Seq.iter *)
val to_seq : 'a stream -> 'a Seq.t
(** Translates an ['a stream] into an ['a Seq.t] *)
val of_seq : 'a Seq.t -> 'a stream
(** Translates an ['a Seq.t] into an ['a stream]
@raise Failure if the input sequence is finite. *)
Tip: Use let ... = patterns.
type 'a cons = Cons of 'a * 'a stream
and 'a stream = unit -> 'a cons
let hd (seq : 'a stream) = let (Cons (x, _)) = seq () in x
let tl (seq : 'a stream) = let (Cons (_, seq)) = seq () in seq
let rec take n seq = if n = 0 then [] else let (Cons (x, seq)) = seq () in x :: take (n - 1) seq
let rec unfold f x () = let (y, x) = f x in Cons (y, unfold f x)
let bang x = unfold (fun x -> (x, x)) x
let ints x = unfold (fun x -> (x, x + 1)) x
let rec map f seq () = let (Cons (x, seq)) = seq () in Cons (f x, map f seq)
let rec filter p seq () = let (Cons (x, seq)) = seq () in let seq = filter p seq in if p x then Cons (x, seq) else seq ()
let rec iter f seq = let (Cons (x, seq)) = seq () in f x; iter f seq
let to_seq seq = Seq.unfold (fun seq -> Some (hd seq, tl seq)) seq
let rec of_seq seq () = match seq () with
| Seq.Nil -> failwith "Not a infinite sequence"
| Seq.Cons (x, seq) -> Cons (x, of_seq seq)
Diagonal of a Sequence of Sequences
Write a function diag : 'a Seq.t Seq.t -> 'a Seq that returns the diagonal
of a sequence of sequences. The returned sequence is formed as follows:
The first element of the returned sequence is the first element of the first
sequence; the second element of the returned sequence is the second element of
the second sequence; the third element of the returned sequence is the third
element of the third sequence; and so on.
let rec diag seq_seq () =
let hds, tls = Seq.filter_map Seq.uncons seq_seq |> Seq.split in
let hd, tl = Seq.uncons hds |> Option.map fst, Seq.uncons tls |> Option.map snd in
let d = Option.fold ~none:Seq.empty ~some:diag tl in
Option.fold ~none:Fun.id ~some:Seq.cons hd d ()